簡介
重尾分布又可以分為兩個子類型,分別是長尾分布(long-tailed distributions)以及次指數分布(subexponential distributions)。
定義
在一個累積分布函式中,一個隨機變數 X 的分布狀況,在以下狀況時,被稱為是一個重尾分布。假設:
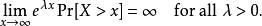 重尾分布
重尾分布如果以尾部分布函式的方式來呈現時,
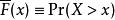 重尾分布
重尾分布最後可以被寫成:
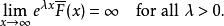 重尾分布
重尾分布 重尾分布
重尾分布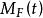 重尾分布
重尾分布這相當於一個動差生成函式, ,對所有的 t>0 來說,都是無限的。重尾分布的左尾,與雙尾分布,定義相同 。
解釋
重尾分布意味著可以更大的機率獲得很大的值. 因此與弱隨機性相反,重尾分布一般表示病態,增加的各種結果被確定為具有重尾分布,包括收入分布、財務報告、保險支出、網頁的參考連結等。重尾分布的一個特殊的子集是冪律,其意味著機率密度函式是一個冪。 一個技術難題是,不是所有的矩存在於這些分布,這一般意味著它們使用分位數和其它順序統計學。這也就是說,中心極限定理不再成立。但是對於諸如均值,即穩定分布的線性組合,我們獲得一個新的標準極限分布。
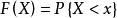 重尾分布
重尾分布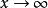 重尾分布
重尾分布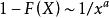 重尾分布
重尾分布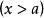 重尾分布
重尾分布設X是一個隨機變數, 為它的分布函式,如果當 時 稱X的分布為重尾分布,又稱冪律分布。
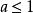 重尾分布
重尾分布一般來說,服從重尾分布的隨機變數X具有較大甚至是無窮大的方差,而且當 時,X的均值也是無窮的。隨機變數X會以不可忽略的機率取到非常大的數值,即:大量的小抽樣取值和少量的大抽樣取值並存。
分類
1.長尾分布
在一個累積分布函式中,一個隨機變數 X的分布,出現以下狀況時,被稱為是一個 長尾分布。假設對所有 t>0 :
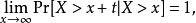 重尾分布
重尾分布這相等於
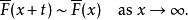 重尾分布
重尾分布對一個右尾部形成長尾分布的狀況,我們可以做一個直觀的解釋:假如一個長尾分布的尾部數量超過某個很高的水準,它超過另一個更高水準的機率會接近於一。也就是說,如果你發現狀況很糟,它可能會比你想像的還要糟。
長尾分布是重尾分布中的一個特例。所有的長尾分布都是重尾分布,但反之則不然,也就是說,我們可以找出某一個重尾分布,它不是長尾分布。
次指數分布
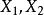 重尾分布
重尾分布 重尾分布
重尾分布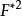 重尾分布
重尾分布次指數分布是以機率分布的折積定義出來的。兩個獨立、不同的隨機變數的共同分布函式 ,它自己的折積定義為,使用勒貝格-史台傑斯積分(Lebesgue–Stieltjes integration) 定義為:
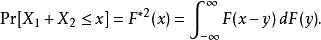 重尾分布
重尾分布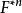 重尾分布
重尾分布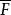 重尾分布
重尾分布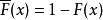 重尾分布
重尾分布n-fold折積的 也以同樣方式定義。其尾端分布函式定義為{。
 重尾分布
重尾分布當以下式子成立,機率分布函式在正的中線上,被定義為 次指數分布:
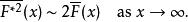 重尾分布
重尾分布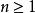 重尾分布
重尾分布這也意味著,對所有來說:
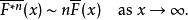 重尾分布
重尾分布