歷史
群的 酉表示是聯繫群論與其它眾多數學分支的重要工具,其中就包括泛函分析尤其是*-代數理論。自20世紀20年代起,該理論首先被廣泛套用於量子力學領域,尤其以《GruppentheorieundQuantenmechanik》最富影響力,Hermann Weyl於1928年出版。作為該領域的先驅之一,George Mackey在20世紀40-60年代發展了酉表示的一般理論,使其研究對象擴展到一般的群而不是僅僅針對某些套用的特殊群 。
值得強調的是群論與泛函分析通過 群的酉表示建立的這種聯繫是相互的。一方面泛函分析尤其是運算元代數方法的引入,使得群論研究的手段和內容都更加豐富。
簡介
 酉表示
酉表示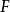 酉表示
酉表示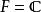 酉表示
酉表示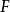 酉表示
酉表示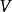 酉表示
酉表示表示論是數學中抽象代數的一支。旨在將抽象代數結構中的元素“表示”成向量空間上的線性變換,並研究這些代數結構上的模,藉以研究結構的性質。略言之,表示論將一代數對象表作較具體的矩陣,並使得原結構中的代數運算對應到矩陣加法和矩陣乘法。此法可施於群、結合代數及李代數等多種代數結構;其中肇源最早,用途也最廣的是群表示論。設 為群,其在域 (常取複數域 )表示是一 矢量空間 及映至一般線性群之群同態
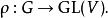 酉表示
酉表示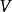 酉表示
酉表示 酉表示
酉表示假設 有限維,則上述同態即是將 的元素映成可逆矩陣,並使得群運算對應到矩陣乘法。
表示論的妙用在於能將抽象代數問題轉為較容易解決的線性代數問題。此外,群還可以表示在無窮維空間上;例如,若考慮無窮維希爾伯特空間上的表示,並要求一些連續性條件,此時表示論就牽涉到一些泛函分析的課題,數學分析的方法就可以用於解決群論的問題。表示論在自然科學中也有套用。對稱性的問題離不開群,而群的研究又有賴於其表示,最明顯的例子便是李群及李代數表示論在量子力學中的關鍵角色。
表示論的一大特點是它遍布數學各個領域。這個特點有兩個方面。首先,表示論的套用十分廣泛:除了在代數的影響之外,表示論
1)通過調和分析闡明並推廣了傅立葉分析;
2)通過不變數理論和愛爾蘭根綱領與幾何學建立了聯繫;
3)通過自守形式和朗蘭茲綱領對數論產生了影響。
常用的表示論包括有限群表示、模表示、 酉表示、李群表示、李代數表示等。
定義
 酉表示
酉表示 酉表示
酉表示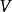 酉表示
酉表示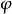 酉表示
酉表示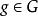 酉表示
酉表示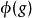 酉表示
酉表示群 的 酉表示是 在實或(通常是)復希爾伯特空間 上的表示 ,使得對於所有 、 都是一個酉運算元。自1920年代起,受赫爾曼·外爾的影響,酉表示廣泛地套用於量子力學,並因此啟發了酉表示理論的發展,主要由尤金·維格納對龐加萊群表示的分析推動。喬治·麥基是建立酉表示的一般理論的先驅之一,而到了1950和1960年代,錢德拉等人建成了一套全面的理論 。
 酉表示
酉表示 酉表示
酉表示 酉表示
酉表示 酉表示
酉表示 酉表示
酉表示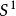 酉表示
酉表示 酉表示
酉表示 酉表示
酉表示酉表示論的主要目標之一是描述“酉對偶”,即 的所有不可約酉表示的空間。酉表示理論最完善的一部分是在 局部緊豪斯多夫拓撲群、表示為強連續映射的情況下。若 是阿貝爾群,那么酉對偶就是特徵標的空間,而當 是緊緻群時,彼得-外爾定理聲明不可約酉表示都是有限維表示,並且酉對偶是離散的。例如,若 是圓群 ,那么特徵標是由整數給出的,因此 的酉對偶就是 。
 酉表示
酉表示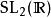 酉表示
酉表示對於非緊緻的 ,酉表示的判定是個微妙的問題。雖然不可約酉表示必須是“可容許表示”(例如錢德拉模),並且要檢測出可容許表示是否具有非退化的不變半雙線性形式是比較容易的,然而要判斷這個形式是否正定卻非常困難。對酉對偶進行有效的描述,哪怕只是對於實半單李群(見下文)等相對規整的群的情況,仍然是表示論中的一個重要的開放問題。這個問題對於許多特殊的群,例如2次特殊線性群 以及洛侖茲群等,已有解答。
分類
1.幾乎酉表示
從群表示論的觀點出發,一對交換矩陣可以理解成由兩個生成元生成的自由交換群的表示,則一對幾乎可交換矩陣可以看成是對這種表示的推廣。因此群的幾乎酉表示的概念就自然產生了。
2.漸進酉表示
在幾乎酉表示的基礎之上,V. M. Manuilov進而給出如下漸進酉表示的概念。
Γ的任意幾乎酉表示都可以納入到一個漸進酉表示當中去。有限生成群的例子有自由群、有限群、交換群以及二維可定向流形的基本群等。
