定義
循環表示是一類簡單的酉表示。
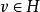 循環表示
循環表示 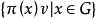 循環表示
循環表示 設 (π,H) 是局部緊群 G 的一個酉表示,若存在,使得生成的子空間在 H 中是稠密的,則稱 π 為循環表示,v 稱為 π 的循環向量。
任一酉表示是循環表示的直和。
拓撲群的酉表示
(unitary representation of topological group)
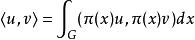 循環表示
循環表示 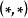 循環表示
循環表示 拓撲群的 酉表示是拓撲群的一類重要表示。局部緊、豪斯多夫群 G 的酉表示是 G 有一個希爾伯特空間 H 上的表示 ,而且滿足:對任意 x∈G,(x) 是 H 的酉運算元。當 G 為緊群時,對 G 的任一有限維表示 (,V) 都可以在 V 中引入新內積使 成為酉表示,其中可取 V 中任一個埃爾米特內積。因此,緊群的表示可以歸結為酉表示。
群的 酉表示是聯繫群論與其它眾多數學分支的重要工具,其中就包括泛函分析尤其是*-代數理論。自20世紀20年代起,該理論首先被廣泛套用於量子力學領域。作為該領域的先驅之一,George Mackey在20世紀40-60年代發展了酉表示的一般理論,使其研究對象擴展到一般的群而不是僅僅針對某些套用的特殊群。

