邏輯符號

邏輯符號在邏輯中，經常使用一組符號來表達邏輯結構。因為邏輯學家非常熟悉這些符號，他們在使用的時候沒有解釋它們。所以，給學邏輯的人的下列表格，列出了最常用的符號、它們的名字、讀法和有關的數學領域。此外，第三列包含非正式定義，第四列給出簡短的例子。

基本符號查看

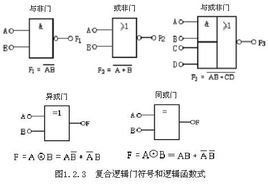
以下為基本邏輯符號

。

符號	名字	解說	例子	讀作	範疇
⇒	實質蘊涵	A ⇒ B 意味著如果 A 為真，則 B 也為真；如果 A 為假，則對 B 沒有任何影響。	x = 2 ⇒ x² = 4 為真，但 x² = 4 ⇒ x = 2 一般為假(因為 x 可以是 −2)。	蘊涵；如果.. 那么	命題邏輯
→		可能意味著同 ⇒ 一樣的意思(這個符號也可以 指示函式 的域和 陪域 ；參見 數學符號 表)。
⊃		可能意味著同 ⇒ 一樣的意思(這個符號也可以指示超集)。
⇔	實質等價	A ⇔ B 意味著 A 為真如果 B 為真，和 A 為假如果 B 為假。	x + 5 = y +2 ⇔ x + 3 = y	若且唯若；iff
↔
¬	邏輯否定	陳述 ¬A 為真，若且唯若 A 為假。	¬(¬A) ⇔ A	非
~	命題邏輯	穿過其他算符的斜線同於在它前面 放置的"¬"。	x ≠ y ⇔ ¬(x =~y)
∧	邏輯合取	如果 A 與 B 二者都為真，則陳述 A ∧ B 為真；否則為假。	n < 4 ∧ n >2 ⇔ n = 3（當 n 是自 然數的時候）。	與
∨	邏輯析取	如果 A 或 B 或二者均為真陳述，則 A ∨ B 為真；如果二者都為假，則 陳述為假。	n ≣ 4 ∨ n ≢ 2 ⇔ n ≠ 3（當 n 是 自然數的時候）。	或
⊕	xor	陳述 A ⊕ B 為真，在要么 A 要么 B 但不是二者為真的時候為真。A ⊻ B 意思相同。	(¬A) ⊕ A 總是真，A ⊕ A 總是假。	異或	命題邏輯, 布爾代數
⊻
∀	全稱量詞	∀ x: P(x) 意味著所有的 x 都使 P(x) 都為真。	∀ n ∈ N（n² ≣ n）.	對於所有； 對於任何；對於每個	謂詞邏輯
∃	存在量詞	∃ x: P(x) 意味著有至少一個 x 使 P(x) 為真。	∃ n ∈ N（n 是偶數）。	存在著
∃!	唯一量詞	∃! x: P(x) 意味著精確的有一個 x 使 P(x) 為真。	∃! n ∈ N（n + 5 = 2n）.	精確的存在一個
:=	定義	x := y 或 x ≡ y 意味著 x 被定義為 y 的另一個名字(但要注意 ≡ 也可以意味著其他東西，比如全等)。	cosh x := (1/2)(exp x + exp (−x))	被定義為	所有地方
≡
:⇔		P :⇔ Q 意味著 P 被定義為邏輯等價於 Q。	A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)
()	優先組合	優先進行括弧內的運算。	(8/4)/2 = 2/2 = 1, 而 8/(4/2) = 8/2 = 4。	無
├	推論	x ├ y 意味著 y 推導自 x。	A → B ├ ¬B → ¬A	推論或推導	命題邏輯, 謂詞邏輯

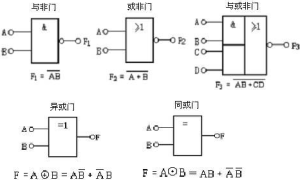邏輯符號