定義
假設有一個值 a以及它的近似值 b，那么 絕對誤差就是
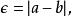逼近誤差相對誤差是
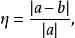逼近誤差百分誤差是
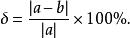逼近誤差其中豎線表示絕對值， a表示真值， b表示 a的近似值。
數值分析
數值分析（英語： numerical analysis），是指在數學分析（區別於離散數學）問題中，對使用數值近似（相對於一般化的符號運算）算法的研究。
逼近誤差 逼近誤差巴比倫泥板YBC 7289是關於數值分析的最早數學作品之一，它給出了在六十進制下的一個數值逼近，是一個邊長為1的正方形的對角線，在公元前1800年巴比倫人也已在巴比倫泥板上計算勾股數（畢氏三元數）（3, 4, 5），即直角三角形的三邊長比。
逼近誤差 逼近誤差數值分析延續了實務上數學計算的傳統。巴比倫人利用巴比倫泥板計算的近似值，而不是精確值。在許多實務的問題中，精確值往往無法求得，或是無法用有理數表示（如）。數值分析的目的不在求出正確的答案，而是在其誤差在一合理範圍的條件下找到近似解。
在所有工程及科學的領域中都會用到數值分析。像天體力學研究中會用到常微分方程，最最佳化會用在資產組合管理中，數值線性代數是資料分析中重要的一部分，而隨機微分方程及馬爾可夫鏈是在醫藥或生物學中生物細胞模擬的基礎。
在電腦發明之前，數值分析主要是依靠大型的函式表及人工的內插法，但在二十世紀中被電腦的計算所取代。不過電腦的內插算法仍然是數值分析軟體中重要的一部分。
誤差
誤差(errors)是實驗科學術語。指測量結果偏離真值的程度。對任何一個物理量進行的測量都不可能得出一個絕對準確的數值，即使使用測量技術所能達到的最完善的方法，測出的數值也和真實值存在差異，這種測量值和真實值的差異稱為誤差。 數值計算分為 絕對誤差和 相對誤差。也可以根據 誤差來源分為 系統誤差（又稱 可定誤差、已定誤差）、 隨機誤差（又稱 機會誤差、未定誤差）和 毛誤差(又稱 粗差)。
參閱
•算法
•計算科學
•數值分析主題列表
•格拉姆－施密特正交化
•數值微分
