定理及其證明
定理:一個有向圖是強連通的,若且唯若G中有一個迴路,它至少包含每個節點一次。
證明:
(1)充分性:如果G中有一個迴路,它至少包含每個節點一次,則G中任兩個節點都是互相可達的,故G是強連通圖。
(2)必要性:如果有向圖是強連通的,則任兩個節點都是相互可達。故必可做一迴路經過圖中所有各點。若不然則必有一迴路不包含某一結點v,並且v與迴路上的個節點就不是相互可達,與強連通條件矛盾 。
強連通圖的邊問題
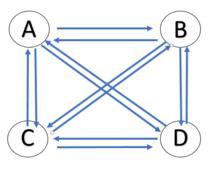 圖1
圖1有n個頂點的強連通圖最多有n(n-1)條邊,最少有n條邊。
(1)最多的情況:即n個頂點中兩兩相連,若不計方向,n個點兩兩相連有n(n-1)/2條邊,而由於強連通圖是有向圖,故每條邊有兩個方向,n(n-1)/2×2=n(n-1),故有n個頂點的強連通圖最多有n(n-1)條邊。
(2)最少的情況:即n個頂點圍成一個圈,且圈上各邊方向一致,即均為順時針或者逆時針,此時有n條邊。
下面舉例說明:如圖1所示,設ABCD四個點構成強連通圖,則:
(1)邊數最多有4×3=12條,如圖1所示。
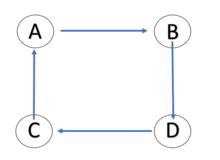 圖2
圖2(2)邊數最少有4條,如圖2所示。
強連通圖的判斷
問題:給一個有向圖,判斷給圖是否是強連通的。
如圖3所示,則是一個強連通圖。
對於無向圖則比較簡單,只需要從某一個頂點出發,使用BFS或DFS搜尋,如果可以遍歷到所有的頂點,則給定的圖是連通的。
但這種方法對有向圖並不適用,例如 : 1 -> 2 -> 3 -> 4,並不是強連通圖。
方法一
可以調用DFS搜尋 V 次,V是頂點的個數,就是對每個頂點都做一次DFS搜尋,判斷是否可達。這樣的複雜度為O(V*(V+E))。
方法二
可以參考求解連通分量的算法Tarjan算法,我們可以在O(V+E) 的時間內找到所有的連通分量,如果連通分量的個數為1,則說明該圖是強連通的。