概念
 透視變換
透視變換透視變換是中心投影的射影變換,在用非齊次射影坐標表達時是平面的分式線性變換。
透視變換常用於,例如在移動機器人視覺導航研究中,由於攝像機與地面之間有一傾斜角,而不是直接垂直朝下(正投影),有時希望將圖象校正成正投影的形式,就需要利用透視變換。
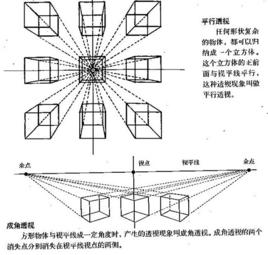
把空問坐標系中的三維物體或對象轉變為二維圖像表示的過程稱為投影變換。根據視點(投影中心)與投影平面之間距離的不同,投影可分為平行投影和透視投影,透視投影即透視變換。平行投影的視點(投影中心)與投影平面之間的距離為無窮大,而對透視投影(變換),此距離是有限的。透視投影具有透視縮小效應的特點,即三維物體或對象透視投影的大小與形體到視點(投影中心)的距離成反比。例如,等長的兩直線段都平行於投影面。但離投影中心近的線段透視投影大,而離投影中心遠的線段透視投影小。該效應所產生的視覺效果與人的視覺系統類似。與平行投影相比,透視投影的深度感更強,看上去更真實,但透視投影圖不能真實地反映物體的精確尺寸和形狀。
分類
對於透視投影,一束平行於投影面的平行線的投影可保持平行,而不平行於投影面的平行線的投影會聚集到一個點,該點稱為滅點(Vanishing Point)。可將滅點看作是無限遠處一點在投影面上的投影。透視投影的滅點可以有無限多個,不同方向的平行線在投影面上就能形成不同的滅點,坐標軸方向的平行線在投影面上形成的滅點又稱作主滅點。透視投影按主滅點的個數可分為一點透視、二點透視和三點透視。
以一點透視為例。一點透視只有一個主滅點,即投影面與一個坐標軸正交.與另外兩個坐標軸平行。進行一點透視投影變換,要很好地考慮圖面布局,以避免三維形體或對象的平面域或直線積聚成點而影響直觀性。具體地說,就是要考慮下列幾點:①三維形體或對象與畫面的相對位置;②視距,即視點(投影中心)與投影面的距
離;③視點的高度。
特點
透視變換同樣是一種改變對象尺寸和形狀的操作,一個平面圖形經透視變換後可產生立體效果。以矩形為例,錯切變換隻移動同一條邊上的兩個頂點,且這兩個頂點的移動方向相同,對邊的兩個頂點保持不動。但是,透視變換可能要移動矩形的全部頂點,且同一邊上兩個頂點的移動方向相反。
事實上,在對象作透視變換時,其限制框的四個角點不一定非要限制在它們的邊長方向,四個角點也可發生移動,從而獲得更複雜的透視變換效果。
線性變換的最一般形式是透視變換。其主要特點是,直線經變換後仍然是直線,但平行的直線經變換後卻可能相交。對於斷層成象圖象數據的處理透視變換用處不是很大。透視變換主要用在如下幾方面:
(1)點源與物體作用,在一個平面上產生投影圖象的放射成象。
(2)對於照片,採集光線全部通過透鏡的焦點的情況。