簡介
幾何變換不改變圖像的像素值， 只是在圖像平面上進行像素的重新安排。適當的幾何變換可以最大程度地消除由於成像角度、透視關係乃至鏡頭自身原因所造成的幾何失真所產生的負面影響。幾何變換常常作為圖像處理套用的預處理步驟， 是圖像歸一化的核心工作之一。
一個幾何變換需要兩部分運算：首先是空間變換所需的運算， 如平移、縮放、旋轉和正平行投影等， 需要用它來表示輸出圖像與輸入圖像之間的(像素)映射關係；此外，還需要使用灰度插值算法， 因為按照這種變換關係進行計算， 輸出圖像的像素可能被映射到輸入圖像的非整數坐標上。
幾何變換的定義
設原圖像f(x0,y0)經過幾何變換產生的目標圖像為g(x1,y1)，則該空間變換(映射)關係可表示為：
x1=s(x0,y0) (1)
y1=t(x0,y0) (2)
其中，s(x0,y0)和t(x0,y0)為由f(x0,y0)到g(x1,y1)的坐標變換函式。
幾何變換算法
根據空間變換的映射關係，確定變換後目標圖像的大小(行、列範圍);//有些變換可能改變圖像大小
計算逆變換(j1,i1)和(j1,i1);
逐行掃描目標圖像g(x1,y1)，對於g(x1,y1)中的每一點(j0,i0);
{
根據空間變換的映射關係，計算得：
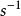幾何變換算法j0'= (j1,i1);//直接通過映射關係計算得到的橫坐標，可能不是整數
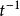幾何變換算法i0'= (j1,i1);//直接通過映射關係計算得到的縱坐標，可能不是整數
根據選用的插值方法:
(j0,i0)=interp(j0',i0');//對於非整數坐標(j0',i0')需要插值
If (j0,i0)在圖像f之內
拷貝對應像素:g(j1,i1)-f(j0,i0);
Else
g(j1,i1)=255;
空間變換運算
平移
平移就是將圖像中所有的點按照指定的平移量水平或者垂直移動。設(x0,y0,z0)為原圖像上的一點，則將點(x0,y0,z0)平移至點(x1,y1,z1)的變換公式為：
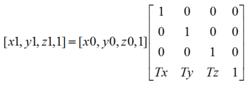幾何變換算法其中，Tx、Ty、Tz分別為圖像在x、y、z方向上的平移分量。
對於原圖中被移出圖像顯示區域的點通常也有兩種處理方法：直接丟棄或者通過加目標圖像的尺寸（將新生成的圖像寬度增加）使新圖像中能夠包含這些點。
縮放
縮放是指圖像大小按照指定的比率放大或者縮小。縮放變換公式為：
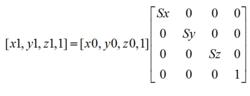幾何變換算法其中，Sx、Sy、Sz是在x、y、z方向上的縮放因子。
直接根據縮放公式計算得到的目標圖像中，某些映射源坐標可能不是整數，從而找不到對應的像素位置。例如，當 時，圖像放大2倍，放大圖像中的像素（0, 1, 2）對應於原圖中的像素（0, 0.5, 1)，這不是整數坐標位置，自然也就無法提取其灰度值。因此我們必須進行某種近似處理即使用插值法處理。
旋轉
旋轉一般是指將圖像圍繞某一指定點旋轉一定的角度。旋轉通常也會改變圖像的大小，可以把轉出顯示區域的圖像截去， 也可以改變輸出圖像的大小以擴展顯示範圍。
對於三維圖像變換，可將其看成分別以x、y、z軸為旋轉軸的3次旋轉組成，依照3種變換關係順序合成。假定在右手坐標系中，物體旋轉的正方向為右手螺旋方向，那么：
幾何變換算法(1) 繞x軸正向旋轉度：
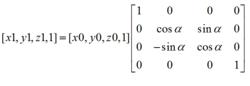幾何變換算法
幾何變換算法(2) 繞y軸正向旋轉度：
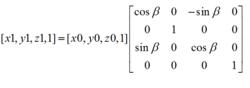幾何變換算法
幾何變換算法(3) 繞z軸正向旋轉度：
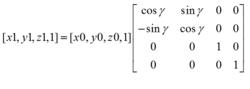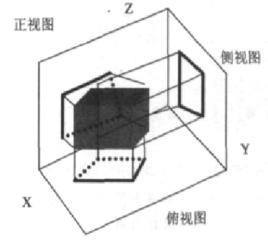
幾何變換算法正平行投影
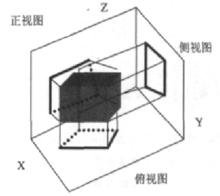圖1 正平行投影示意圖
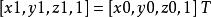幾何變換算法投影方向垂直於投影面。特點是物體的一個坐標面平行於投影面，可以反映出測量形體間的距離，角度和相互位置關係。其變換公式為：，其中，T為變換矩陣。
(1) 正視圖(主視圖、正面投影)：此時視線與y軸平行，視圖反映了實長(x方向)與高(z方向)，而實寬(y方向)則被禁止了。此時變換矩陣T為：
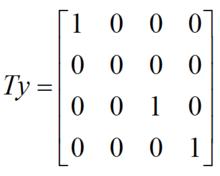幾何變換算法(2) 側視圖(左視圖、側面投影)：此時視線與z軸平行，視圖反映了實長與寬，而高度則不能反映出來。此時變換矩陣為：
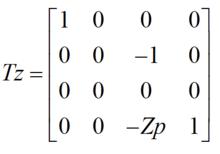幾何變換算法其中-Zp表示俯視方向上的平移量。
(3) 俯視圖(平面圖、水平投影)：此時視線與X軸平行，類似地可以得到變換矩陣為：
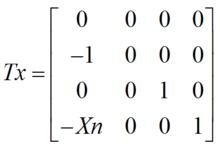幾何變換算法其中，Xn表示側視方向上的平移量。
插值算法
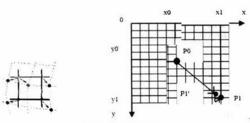圖2 最近鄰插值示意圖最鄰近插值法是一種最簡單的插值算法，輸出像素的值為輸入圖像中與其最鄰近的採樣點的像素值。例如，圖2中的點P0在幾何變換中被映射至點P1'，但由於點P1’處於非整數的坐標位置，無法提取其像素灰度值。所以可以用與P1'最鄰近的採樣點P1的灰度值近似作為P1'的灰度值。
最近鄰插值可表示為：f(x,y)=g(round(x)，round (y))。最近鄰插值算法計算簡單，且在很多情況下的輸出效果較好。但是，最近鄰插值法會在圖像中產生人為加工的痕跡。
