釋義
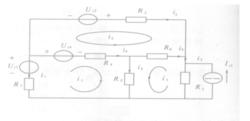 迴路法
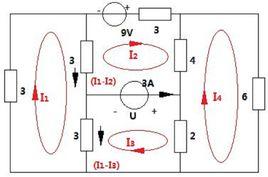
迴路法迴路法是以平面電路或非平面電路的一組獨立迴路電流為電路變數,並對獨立迴路用KVL列出用迴路電流表達有關支路電壓的方程的求解方法。迴路電流是一種沿著迴路邊界流動的假想電流。通常選擇基本迴路為獨立迴路,迴路電流就是相對應的連支電流。如圖所示,設出獨立迴路電流分別為i1、i2、i3。根據迴路法得到的一般規律為:
Ri±Ri=U。(1)
理論詮釋
根據迴路法的定義知,儘管迴路電流是一種沿迴路邊界流動的假想電流,但在上圖中,若選{4、5、6}為樹,則由連支1、2、3與一些樹支可構成3個基本迴路,顯然設定的迴路電流i1、i2、i3即是各相應的連支電流,而樹支電流則由KCL關係得出:
i4=i1-i2,i5=i1+i3,i6=-i3-i2。(2)
(2)式體現了兩層物理含義:
第一,樹支電流等於流經該支路的有關迴路電流的代數和,連支電流即相對應的迴路電流。所以選用迴路電流作變數,則電路中所有支路電流都可用迴路電流表示。
第二,當選用迴路電流作電路變數時,KCL就自動滿足。因此在求解電路時,只需對基本迴路列寫KVL方程即可,這就是其簡單有效性的依據。關於(1)式則要掌握的是:
①路電流的方向即為迴路的繞行方向;
②Rkk稱為迴路k的自電阻,它是迴路k中所有電阻之和,恆取“+”號。如R22=R2+R4+R6;
③Rkj稱為迴路k與迴路j的互電阻,它是迴路k與迴路j共有支路上所有公共電阻的和,如果流過電阻上的兩迴路電流方向相同,其前取“+”;若方向相反,其前取“-”號。如R12=-R4,R13=R5;
④Uskk是迴路k中沿繞行方向所有電源電壓的代數和,如U=U-U
⑤對每個基本迴路列出上述方程,共可列b-n+1個方程。
迴路法步驟
(1)選定一組(b-n+1)個獨立迴路,並標出各迴路電流的參考方向。
(2)以迴路電流的方向為迴路的巡行方向,按照前面的規律列出各迴路電流方程。 自電阻始終取正值,互電阻前的符號由通過互電阻上的兩個迴路電流的流向而定,兩個迴路電流的流向相同,取正;否則取負。等效電壓源是電壓源電壓升的代數和,注意電壓源前的符號。
(3)聯立求解,解出各迴路電流。
(4)根據迴路電流再求其它待求量。