迴路矩陣簡介
通常,一個不可分隔子系統,通常包含若干個再循環迴路,如圖給出的就是一個不可分隔子系統,其中包含有四個再循環迴路。那種包含兩個以上流股,且其中的任何單元只被通過一次,稱作簡單迴路。
過程系統中的簡單迴路可以用迴路矩陣表示。矩陣中行表示迴路 ,列表示物流。若某迴路i中包括有物流j則相應的矩陣元素aij=1,否則為空白或零。
迴路矩陣與迴路電壓定律
關聯矩陣A反映了電路節點與支路之間的連線關係 ,由此可建立矩陣形式的基爾霍夫電流定律。與此相似,當用迴路電流法分析電路時,必須建立迴路與支路之間的關係,如必需知道迴路是由那些支路所組成,支路與迴路之間的參考方向關係。這些關係可以用一個迴路矩陣來描述。的行對應於某一迴路,的列對應於某條支路,矩陣的元素滿足以下關係:
矩陣充分反映了迴路與支路的關聯情況。
在用迴路電流法分析計算電路問題時,選取正確合適的獨立迴路是一個重要的問題。對於某一電路,可以選擇許多不同的迴路。如對於所示的網路有向圖,至少可以選擇7條不同的迴路來列寫迴路矩陣。但這樣列出的迴路矩陣中,有些迴路對應的中的行是線性相關的,即是說中的某些行可以通過其它行的代數運算而得到。在電路分析中,當用基爾霍夫定律建立迴路方程時,只有一組線性獨立的迴路電壓方程才有實際意義。在前面已討論過如何選取網路的迴路來獲得獨立的基爾霍夫迴路電壓方程,獨立迴路可以選取單連支迴路。選擇單連支迴路來建立的迴路矩陣,稱為基本迴路矩陣,用來表示。
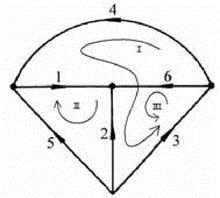 圖示
圖示若選取支路1、2、3作為樹,可寫出它的基本迴路矩陣為:
基本迴路矩陣為階矩陣。矩陣的秩等於矩陣的行數。
上面在對圖7-3-1網路編號時,若支路編號採取先樹支後連支的安排,這樣建立的基本迴路矩陣右半部是一個 l階的單位矩陣( l為連支數)即基本迴路矩陣可以表述為:
這裡要指出的是,迴路矩陣的行反映了某一迴路與支路之間的關係,而迴路矩陣的列則反映了某一支路與所有迴路之間的關係。即是說,從某一列元素中可以看出有多少迴路穿越該支路,且可判別出迴路方向與支路方向之間的關係,它實際上隱含著支路電流與迴路電流之間的關係信息。
對於平面網孔,另一種選取獨立迴路的方法是選擇網孔迴路,由網孔迴路建立的迴路矩陣稱作網孔迴路矩陣,可用來表示。如對於網路,可寫出其網孔迴路矩陣。
這裡取迴路方向為順時針方向。
迴路矩陣的每一行元素反映了該迴路中所包含的支路及其方向。若設網路支路電壓的參考方向與支路電流方向一致,寫成列向量為,用迴路矩陣左乘支路電壓列向量 u,可得個元素的列向量,其中每一行都包含了該迴路中所有支路電壓代數和,且當支路電壓方向與迴路一致時為正,反之為負。由基爾霍夫電壓定律可知,任一閉合迴路的電壓代數和恆為零,因此可知與 u的乘積為零。
對於正弦穩態交流電路。
對於網路,其支路電壓列向量為用前面得到的基本迴路矩陣左乘 u。
乘積的每一行是各迴路中支路電壓代數和,是基爾霍夫電壓定律的反映,矩陣形式的基爾霍夫電壓定律。
下面分析支路電流與迴路電流之間的關係。前面已指出,迴路矩陣的每一列元素實際上是反映某一支路中所穿過的迴路和方向。設迴路電流列向量為,則用左乘後,乘積的每一行之和恰為流過該支路中所有迴路電流的代數和,且迴路電流方向與支路方向一致時為正,反之為負。由迴路電流法解題的知識可知,任一支路中所有迴路電流代數和為該支路電流之值。因此可知與的乘積為支路電流列向量 i ,即:
選單連支迴路為獨立迴路,此時迴路電流即為連支電流。
關聯矩陣、迴路矩陣和割集矩陣的關係
對於同一個電路,若各支路,節點的編號及方向均相同時,其列寫出的關聯矩陣,迴路矩陣和割集矩陣之間存在著一定的聯繫。當採用計算機輔助計算建立狀態方程時,直接寫迴路矩陣或割集矩陣往往比較困難,而推求關聯矩陣卻很方便。因此在實際套用時往往由關聯矩陣求得迴路矩陣與割集矩陣。

