平面直角坐標系中的轉軸公式
設坐標軸的旋轉角為θ，P是平面的任意一點，在原坐標系xOy中的坐標為(x，y)，在新坐標系x′Oy′中的坐標為(x′，y′)(如圖1)，則
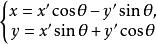轉軸公式或
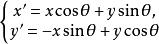轉軸公式叫做坐標軸的旋轉公式，簡稱 轉軸公式。
說明：(1)為便於記憶，可將轉軸公式寫成矩陣形式：
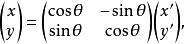轉軸公式或
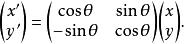轉軸公式矩陣的乘法按如下規定進行：
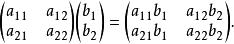轉軸公式(2)逆時針旋轉坐標軸時，旋轉角θ取正值；順時針旋轉坐標軸時，旋轉角θ取負值 。
空間直角坐標系中的轉軸公式
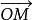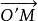轉軸公式
轉軸公式空間直角坐標變換是一類重要的坐標變換，設空間任意一點M在空間直角坐標系{O;i，j，k}的坐標為(x，y，z)，在新坐標系{O′;i′，j′，k′}的坐標為(x′，y′，z′).即有=xi+yj+zk，=x′i′+y′j′+z′k′。又設新原點O′在舊坐標系中的坐標為(h，h，h)，新坐標系的基i′，j′，k′在舊坐標系中的方向餘弦為(cos α，cos β，cos γ) (i=1，2，3)，即：
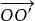轉軸公式=hi+hj+hk，
i′=i cos α+j cos β+k cos γ，
j′=i cos α+j cos β+k cos γ，
k′=i cos α+j cos β+k cos γ.
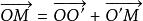轉軸公式將(cos α，cos β，cos γ)改記為(ccc) (i=1，2，3)，則由得
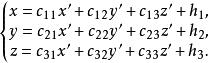轉軸公式這就是 空間直角坐標變換公式。其中的9個係數c並不互相獨立，由於i，j，k和i′，j′，k′都是由互相正交的單位向量組成的標準正交基，方向餘弦c滿足下列6個正交條件：
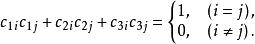轉軸公式對應的係數矩陣(c)是正交矩陣，即(c) (c)=I.特別地，當(c)=I，即坐標變換公式為
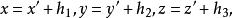轉軸公式此式稱為坐標軸的平移公式，簡稱 移軸公式。而當(h，h，h)=(0，0，0)時，則坐標變換公式為
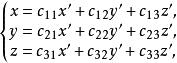轉軸公式即
轉軸公式此式稱為坐標軸的旋轉公式，簡稱 轉軸公式。因新、舊坐標系皆為右手系，故det(c)=1 。
