輔助角

在和差化積問題中，有些和差形式的表達式不能直接套用和差化積公式，但引進適當的輔助角後就可容易地將它們化為乘積形式。在一般形式的引人輔助角的變換可以說明如下：將已知數或已知式考慮成某個自變數的三角函式值，這個自變數叫做輔助角(輔助自變數)。從輔助角的所有可能值的集合中取出一個完全確定的值(例如，絕對值最小的值)。這樣選好後，輔助角它的三角函式的給定值，可以完全確定，並且在以後的變換式中就看成是已知的 。

基本介紹

在和差化積問題中，有些和差形式的表達式不能直接套用和差化積公式，但引進適當的輔助角後就可容易地將它們化為乘積形式，這裡給出幾種常見的引進輔助角的方法 。

常見引入輔助法的方法

asinx+bcosx (a、b是非零實數)

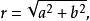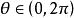輔助角

輔助角

在直角坐標系中，設點M的坐標是(a，b)，a，b≠0，並記 那么存在唯一的 使得

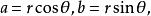輔助角

從而

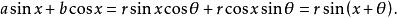輔助角

注意：上面這種變形常用於有關振動的問題中。若考慮點N(b，a)，令

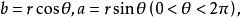輔助角

則

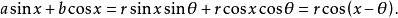輔助角

a±b(a、b是非零實數)

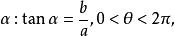輔助角

引進角則

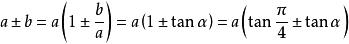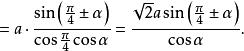輔助角

輔助角

a²-b² (a、b是非零實數，|b|

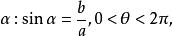輔助角

若引進角則

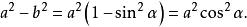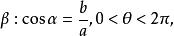輔助角

輔助角

若引進角則

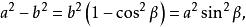輔助角

或者

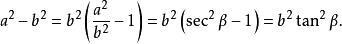輔助角

a²+b² (a、b是非零實數)

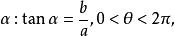輔助角

引進角則

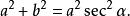輔助角

例題解析

將下列二式化為乘積形式：

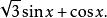輔助角

（1）

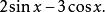輔助角

（2）

解：（1）我們有

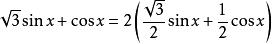輔助角

輔助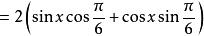角

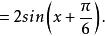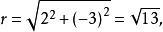輔助角

輔助角

（2）取參照本題（1），則有

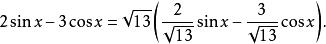輔助角