定律定義
軌道-穩定集定理(Orbit-stabilizer theorem) 設G是[1,n]上的一個置換群，Ek是[1,n]在G的作用下包含k的等價類，Zk是k不動置換類 。有|Ek||Zk|=|G|.
推導過程
證明：
設|Ek|= l,Ek={a1(=k),a2,…,a l} k=a1→ai,
i=1,2,…, l. P={p1,p2,…,p l}
令Gi=Zp,i=1,2,…, l.則k在Zp的作用下變為a
GiÍG(G關於Z的陪集分解)i≠j,Gi∩Gj=Φ.
軌道-穩定集定理G1+G2+…+Gl G.
另一方面，任意p∈G. k→aj→k
PPj∈Zk, P∈ZkPj=Gj.
∴ G Í G1+…+G.
從而，G=G1+G2+…+Gl.
|G|=|G1|+|G2|+…+|G l|=|Zp|+| Zp|+…+| Zp |
= |Zk|· l= |Zk|·|Ek|.證畢。
實驗驗證
考慮正方形頂點二著色問題
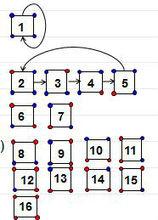軌道-穩定集定理·|G|:置換個數 –只考慮旋轉: 4
·置換群
–Rotate 0 degree: p0=(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)
(13)(14)(15)(16)
–rotate 90 degree:
p1=(1)(2 3 4 5)(6 7)(8 9 10 11)(12 13 14 15)(16)
–rotate 180 degree:
p2=(1)(2 4)(3 5)(6)(7)(8 10)(9 11)(12 14)(13 15)(16)
–rotate 270 degree:
p3=((1)(2 5 4 3)(6 7)(8 11 10 9)(12 15 14 13)(16)
不動置換類 Z1={p0, p1, p2, p3}=4
等價類：E1=1
E1 *Z1 = |G| =4
套用領域
組合數學 群論
定律影響
是burnside引理 的基礎
