概念
超越基(transcendence basis)亦稱極大超越集。域論的基本概念之一。它是線性代數中基概念的推廣,是擴域的極大代數無關集。設K是域F的擴域,K的一個子集S稱為K在F上的超越基,是指:S在F上代數無關,K是F(S)的代數擴域。域F的任一擴域K都存在超越基。超越基不是惟一的,但它的基數相等,稱此基數為K在F上的超越次數,記為tr.degK或tr.deg(K/F)。若L是F的擴域,K為中間域,則:
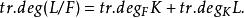 超越基
超越基代數擴域的超越基為空集,它的超越次數規定為零。
基
代數數域作為有理數域上的線性空間的基。設K=Q(θ)為n次代數數域,記θ=θ ,並以θ ,…,θ 表示θ所適合的不可約多項式的其他n-1個根。於是,K中任一數α必可表為α=α(θ)=a+aθ+…+aθ ,其中a為有理數。設α =α,則稱α =α(θ )(k=2,3,…,n)為α的共軛數,稱S(α)=α +α +…+α =α(θ )+α(θ )+…+α(θ )與N(α)=α ,α ,…,α =α(θ ),α(θ ),…,α(θ )為α的跡與范。有S(α+β)=S(α)+S(β), N(αβ)=N(α)N(β).S(α),N(α)均為有理數。特別地,若α為有理數時,則S(α)=nα,N(α)=α。若α為代數整數,則S(α),N(α)均為代數整數,從而為有理整數。若在K中能找到一組數α,α,…,α,使K中任何一數都可以惟一地表為aα+aα+…+aα的形式,其中a(1≤j≤m)為有理數,則稱α,α,…,α為K之基.K中任何基所含元素個數相同,且均等於n。若α,α,…,α及β,β,…,β為R(θ)之兩組基,則有有理數a(1≤j,k≤n)使:
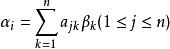 超越基
超越基且其係數行列式|a|≠0。
域論
域論(Field Theory)是抽象代數的分支,研究域的性質。簡單地說,一個域是在其上有"加法"、"減法"、"乘法"和"除法"的代數結構。
域的概念最初被阿貝爾和伽羅瓦隱含地用於他們各自對方程的可解性的工作上。
1871年,理察·戴德金將對於四則運算封閉的實數或複數集稱為“域”。
1881年,利奧波德·克羅內克定義了“有理域”(英文:domain of rationality,德文:Rationalitäts-Bereich),相當於今稱之數域。
1893年,安里西·韋伯給出抽象域的首個清晰定義。
1910年,施泰尼茨於1911年發表了論文《域的代數理論》(英文:Algebraic Theory of Fields、德文:Algebraische Theorie der Körper)。論文中他以公理化的方式研究了域的性質並給出了多個域的有關術語,比如素域、完全域,和域擴張的超越次數。
雖然伽羅瓦並未提出域的概念,但一般被譽為是首個將群論和域論連繫起來的數學家,伽羅瓦理論便以他命名。事實上,埃米爾·阿廷在1928至42年間才將群和域的關係大大地發展。
擴域
域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
若域E是F的擴域,K是E的擴域,則稱E是域擴張K/F的中間域。若K/F是域擴張,S是K的子集,且F(S)是K的含F與S的最小子域,稱F(S)為F添加S的擴域。當S={α,α,…,α}是有限集合時,F(α,α,…,α)稱為添加α,α,…,α於F的有限生成擴域(或者F上的有限生成擴張).它由一切形如:
f(α,α,…,α)/g(α,α,…,α)
的元組成,其中α,α,…,α∈S,f,g是F上的n元多項式且:
g(α,α,…,α)≠0.
由於這個原因,當F(α,α,…,α)關於F的超越次數≥1時,F(α,α,…,α)也稱為F上的代數函式域。當S={α}時,稱F(α)為F的單擴張域,也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是,擴域K與基域間存在有限箇中間域。這是施泰尼茨(Steinitz,E.)證明的。
