定義
二階線性微分方程
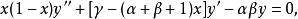 超幾何方程
超幾何方程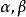 超幾何方程
超幾何方程 超幾何方程
超幾何方程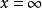 超幾何方程
超幾何方程其中和為任意參數,被稱為 超幾何方程.它在x=0,x=1和有奇點.
此外,任意齊次線性二階微分方程
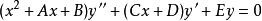 超幾何方程
超幾何方程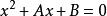 超幾何方程
超幾何方程 超幾何方程
超幾何方程 超幾何方程
超幾何方程可被轉換為超幾何方程,前提是方程有兩個不同的根和.重寫上述超幾何方程在如下定義的新的自變數t下
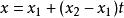 超幾何方程
超幾何方程得
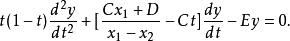 超幾何方程
超幾何方程其中設
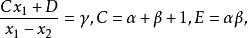 超幾何方程
超幾何方程再次用x表示新變數t 即得到超幾何方程.
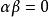 超幾何方程
超幾何方程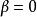 超幾何方程
超幾何方程如果則超幾何方程通過兩次積分是可解的.如並積分方程
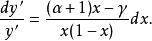 超幾何方程
超幾何方程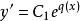 超幾何方程
超幾何方程得到,其中
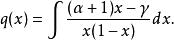 超幾何方程
超幾何方程則二次積分得到
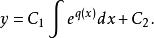 超幾何方程
超幾何方程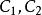 超幾何方程
超幾何方程均為常數。
在超幾何方程理論中,主要強調的是超幾何方程的漸近線和它在單點旁的級數解.但是,實際上經常需要一類超幾何方程的通解解析式.因此,下面的定理決定了一類超幾何方程可以被初等函式可積或是求積.
相關定理
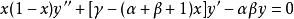 超幾何方程
超幾何方程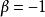 超幾何方程
超幾何方程 超幾何方程
超幾何方程 超幾何方程
超幾何方程超幾何方程在和兩個任意參數和:
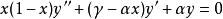 超幾何方程
超幾何方程的通解能通過積分得到,其形式是
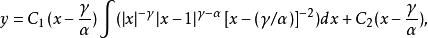 超幾何方程
超幾何方程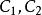 超幾何方程
超幾何方程其中是任意常數。
 超幾何方程
超幾何方程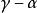 超幾何方程
超幾何方程註: 如果和是有理數,可以通過標準變換將上式中的積分化簡為有理函式的積分並將上式的解表示為初等函式.
