發展簡史
皮埃爾·德·費馬於1636年發現了這個定理。在一封1640年10月18日的信中他第一次使用了上面的書寫方式。在他的信中費馬還提出a是一個素數的要求,但是這個要求實際上是不必要的。
1736年,歐拉出版了一本名為“一些與素數有關的定理的證明”(拉丁文:Theorematum Quorundam ad Numeros PRIMOS Spectantium Demonstratio)”的論文中第一次提出證明,但從萊布尼茨未發表的手稿中發現他在1683年以前已經得到幾乎是相同的證明。
有些學家獨立製作相關的假說(有時也被錯誤地稱為中國的假說),當成立時,p是素數。這是費馬小定理的一個特殊情況。然而,這一假說的前設是錯的:例如,341 ,而341= 11×31是一個偽素數。所有的偽素數都是此假說的反例。
如上所述,中國猜測僅有一半是正確的。符合中國猜測但不是素數的數被稱為偽素數。
更極端的反例是卡麥可數: 假設a與561互質,則 a 被561除都餘1。這樣的數被稱為卡麥可數數,561是最小的卡麥可數。Korselt在1899年就給出了卡麥可數的等價定義,但直到1910年才由卡麥可(Robert Daniel Carmichael)發現第一個卡麥可數:561。1994年William Alford、Andrew Granville及Carl Pomerance證明了卡麥可數有無窮多個。
驗證推導
引理1.
若a,b,c為任意3個整數,m為正整數,且(m,c)=1,則當a·c≡b·c(mod m)時,有a≡b(mod m)。
證明:a·c≡b·c(mod m)可得ac–bc≡0(mod m)可得(a-b)·c≡0(mod m)。因為(m,c)=1即m,c互質,c可以約去,a– b≡0(mod m)可得a≡b(mod m)。
引理2.
設m是一個整數且m>1,b是一個整數且(m,b)=1。如果a[1],a[2],a[3],a[4],…a[m]是模m的一個完全剩餘系,則b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也構成模m的一個完全剩餘系。
證明:若存在2個整數b·a[i]和b·a[j]同餘即b·a[i]≡b·a[j](mod m)..(i>=1 && j>=1),根據引理1則有a[i]≡a[j](mod m)。根據完全剩餘系的定義可知這是不可能的,因此不存在2個整數b·a[i]和b·a[j]同餘。
所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]構成模m的一個完全剩餘系。
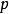 費馬小定理
費馬小定理 構造素數 的完全剩餘系
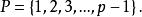 費馬小定理
費馬小定理 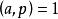 費馬小定理
費馬小定理 因為 ,由引理2可得
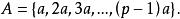 費馬小定理
費馬小定理 也是p的一個完全剩餘系。由完全剩餘系的性質,
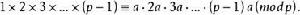 費馬小定理
費馬小定理 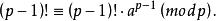 費馬小定理
費馬小定理 即
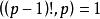 費馬小定理
費馬小定理 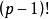 費馬小定理
費馬小定理 易知 ,同餘式兩邊可約去 ,得到
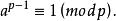 費馬小定理
費馬小定理 這樣就證明了費馬小定理。
定理意義
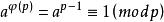 費馬小定理
費馬小定理 費馬小定理是初等數論四大定理(威爾遜定理,歐拉定理(數論中的歐拉定理),中國剩餘定理(又稱孫子定理)之一,在初等數論中有著非常廣泛和重要的套用。實際上,它是歐拉定理的一個特殊情況(即 ,見於詞條“歐拉函式”)。
套用
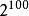 費馬小定理
費馬小定理 計算 除以13的餘數
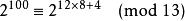 費馬小定理
費馬小定理 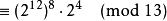 費馬小定理
費馬小定理 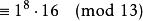 費馬小定理
費馬小定理 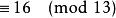 費馬小定理
費馬小定理 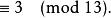 費馬小定理
費馬小定理 故餘數為3。
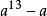 費馬小定理
費馬小定理 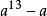 費馬小定理
費馬小定理 證明對於任意整數a而言,恆為2730的倍數。13減1為12,12的正因數有1, 2, 3, 4, 6, 12,分別加1,為2, 3, 4, 5, 7, 13,其中2, 3, 5, 7, 13為質數,根據定理,為2的倍數、為3的倍數、為5的倍數、為7的倍數、為13的倍數,即2*3*5*7*13=2730的倍數。
Python程式碼
>>> n =221
>>>a = 38
>>>pow(a ,n -1,n)
1
"""221 may be a prime number."""
import random
def isprime(n,k=128):
if n

