簡介
在邊坡工程中經常遇到土坡的穩定性分析問題，費倫紐斯(Fellenius)和畢肖普(Bishop)用豎向條分法近似定值地計算了簡單土坡的穩定安全係數，費倫紐斯條分法沒有考慮土條間的相互作用 。費倫紐斯條分法是用極限平衡原理進行粘性土土坡穩定性分析時，當粘性土土坡失穩時，將沿一曲面滑動，通常將滑動曲面簡化為圓弧，當φ=0時，土坡的最危險圓弧滑動面通過坡腳，進行土坡穩定分析的條分法。費倫紐斯條分法沒有考慮土條間的相互作用 ，所以計算結果偏於保守。這種方法不但可用於簡單土坡，也可以用於較複雜的情況。
條分法是土坡穩定分析方法中套用最普遍的一類方法。在條分法中，首先假定可能的滑動面，然後將滑動面以上的土體分成若干垂直土條，再對作用在土條上的力進行平衡分析，建立平衡方程。一般情況下，未知量數大於可建立的方程數，屬超靜定問題。為了使問題有解，在條分法中採用了各種簡化假定以減少未知量數或增加方程數。通過平衡分析求出極限平衡狀態下土體穩定的安全係數，並通過試算找出最危險的滑動面及相應的安全係數。根據不同的簡化假定，條分法可分為瑞典圓弧滑動法， 畢肖普法，摩根斯坦法，楊布普遍條分法，斯賓塞法，不平衡推力傳遞法等。
極限平衡法
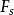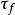費倫紐斯條分法
費倫紐斯條分法
費倫紐斯條分法極限平衡法是建立在Mohr-Coulomb強度準則基礎之上的，將滑體視為剛性體，不考慮其本身的變形，除楔形破壞外，其餘的破壞大多簡化為平面問題。其特點是只考慮靜力平衡條件和土的Mohr-Coulomb破壞準則，通過對可能的滑動面的試算求出最小安全係數，故極限平衡法只能求得一種近似解。但是由於該方法的套用積累了豐富的經驗，而精確合理的方法尚未成熟，所以，在工程實踐中仍廣泛採用極限平衡法，最為常見的極限平衡法是條分法。極限平衡法假設土體的一部分沿著某一滑裂面滑動，在該滑裂面上土體處處達到極限平衡，即正應力和剪應力滿足Mohr-Coulomb強度準則。安全係數的求解則根據Bishop等對土坡穩定安全係數 的定義：沿整個滑裂面的抗剪強度 與實際產生的剪應力 之比，即：
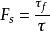費倫紐斯條分法這樣定義的安全係數物理意義更加明確，使用更廣泛，也為以後的各種極限平衡法提供了有利條件。該法將滑坡體分為若干土條，要求對每個土條和整個滑動土體都應滿足靜力平衡條件，還必須滿足兩個合理性條件：土條分界面上不違反土體破壞準則，即沿著劃分的土條兩側面上的剪應力不能超過在這個面上所能發揮的抗剪能力；一般地說，不允許土條之間出現拉力。由於對相鄰土條之間的內力所作假定的不同，所能滿足的靜力平衡條件也不相同，大體可分為：滿足力平衡法、滿足整體力矩平衡法、滿足力和力矩的平衡法三類，它們在實際套用中適合不同場合 。
邊坡
按邊坡的成因可以分為天然邊坡如自然形成的山坡和江河湖海的岸坡和人工邊坡如在路堤、路塹、深基坑等。按構成坡體的岩土的性質可以分為土質邊坡和岩質邊坡。按邊坡的穩定程度可以分為穩定邊坡、基本穩定邊坡、欠穩定邊坡和不穩定邊坡。這種邊坡分類方法一般根據邊坡的穩定安全係數的大小進行劃分，但無嚴格規定。按邊坡的高度分類，邊坡高度大於巧的稱為高邊坡，小於的稱為一般邊坡。根據邊坡的斷面形式可以分為直立式邊坡、傾斜式邊坡和台階式邊坡。根據使用年限，工程邊坡分為臨時性邊坡和永久性邊坡。臨時性邊坡是指工作年限不超過兩年的邊坡永久性邊坡是指工作年限超過兩年的邊坡。土坡穩定問題一般都假定為平面應變問題，早期學者在研究邊坡問題時都假定滑動面是一個圓柱面，土坡的安全係數是用滑動面上全部抗滑力矩和滑動力矩之比定義的。但實際上，即使是簡單均質的土坡，其滑動面也不一定是圓柱面。
