簡介
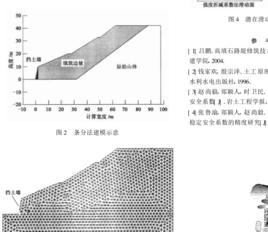
條分法是土坡穩定分析方法中套用最普遍的一類方法。 在條分法中,首先假定可能的滑動面,然後將滑動 面以上的土體分成若干垂直土條,再對作用在土條上的力進行平衡分析,建立平衡方程。一般情況下,未知量數大於可建立的方程數,屬超靜定問題。為了使問題有解,在條分法中採用了各種簡化 假定以減少未知量數或增加方程數。通過平衡分析 求出極限平衡狀態下土體穩定的安全係數,並通過試算找出最危險的滑動面及相應的安全係數。根據 不同的簡化假定,條分法可分為瑞典圓弧滑動法, 畢肖普法,摩根斯坦法,楊布普遍條分法,斯賓塞 法,不平衡推力傳遞法等。
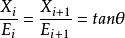 斯賓賽法
斯賓賽法斯賓賽法假定相鄰土條之間的法向條間力E與切向條間力X 之間有一固定的常數關係,即各條間力合力 P 的方向是互相平行的: 。
極限平衡法基本原理
極限平衡法採用條分法進行邊坡的穩定分析計算,該方法先假定若干剪下破壞面,然後將破壞面之上的土體分成若干垂直土條,對作用於各土條上的力和力矩進行平衡分析,求出在極限平衡狀態下的土體安全係數,並通過一系列方法確定最危險滑裂面位置和最小安全係數。極限平衡法的發展經歷了一個漫長的階段。上世紀年代以前,對土質邊坡穩定計算,一律只計土體的內摩擦角,並假定滑動面是平面,1773年法國工程師庫侖和年英國學者朗肯分別提出的土壓力理論就是這類方法的代表。1916年,彼德森和胡爾頓根據大量觀測論證了某些土體特別是有粘結力的土體在發生滑動失穩破壞時,其滑動面是與圓柱面接近的曲面,在此基礎上彼德森提出了圓弧滑面分析法,仍只計土的內摩擦力,並且不考慮土體內部土條間的相互作用力,這就是最初的瑞典圓弧法。30-40年代是瑞典圓弧法逐漸完善的時期,瑞典學者費蘭紐斯將最初的圓弧法推廣到兼有摩擦力和粘結力的土坡穩定計算中去,並初步探索了最危險滑弧位置的變化規律。40年代以後,不少學者致力於改進瑞典圓弧法,主要研究兩個方向一方面,不少學者致力於探索最危險滑弧的位置,製作數表、曲線,以減少計算工作,如泰勒、畢肖普、拉姆里和包洛斯等另一方面,有不少人研究滑裂面的形狀,如太沙基等。50一60年代,人們研究的主攻方向,一是如何在計算中考慮滑動土體內部土條間的相互作用力,二是研究如何將此法推廣套用到任意形狀的滑動面,這一階段的研究成果表現為1954年簡布提出普遍條分法的基本原理,1955年畢肖普明確了土坡穩定安全係數的定義。
邊坡穩定分析的發展現狀
邊坡的穩定分析是岩土工程中的重要研究課題之一,在近百年的發展中,許多研究者致力於這一工作。因此,邊坡穩定分析的內容十分豐富。總體上來說,邊坡穩定分析有兩種方法定性分析法和定量分析法。定性分析法主要是通過工程地質勘察,對影響邊坡穩定性的主要因素、可能的變形破壞方式及失穩的力學機制的分析,對己變形地質體的成因及其演化史進行分析,從而給出被評價邊坡一個穩定性狀況及其可能發展趨勢的定性說明和解釋。定性分析的優點是能綜合考慮影響邊坡穩定性的多種因素,快速地對邊坡的穩定狀況及其發展趨勢作出評價。然而,人們更關心的是如何定量的表示其邊坡的穩定性,即邊坡穩定分析的計算方法。邊坡穩定分析的計算方法有多種,如數值分析方法、塑性極限方法、條分法、可靠度方法和模糊數學方法等。對於土質邊坡來說,為人們所熟知和廣泛討論的方法有條分法和有限元方法。條分法,因為其力學模型簡單適用,可對邊坡進行定量的評價,經過長期的工程實踐和不斷的完善和補充,己經成為邊坡穩定分析的成熟方法。近年來隨著數值分析方法,在工程領域套用技術的成熟,同時為彌補條分法假設上的不足,有限元方法正成為邊坡穩定分析的熱點。