概念
貪婪算法是一種不追求最優解,只希望得到較為滿意解的方法。貪婪算法一般可以快速得到滿意的解,因為它省去了為找最優解要窮盡所有可能而必須耗費的大量時間。貪婪算法常以當前情況為基礎作最優選擇,而不考慮各種可能的整體情況,所以貪婪法不要回溯。
例如平時購物找錢時,為使找回的零錢的硬幣數最少,不考慮找零錢的所有各種發表方案,而是從最大面值的幣種開始,按遞減的順序考慮各幣種,先儘量用大面值的幣種,當不足大面值幣種的金額時才去考慮下一種較小面值的幣種。這就是在使用貪婪算法。這種方法在這裡總是最優,是因為銀行對其發行的硬幣種類和硬幣面值的巧妙安排。如只有面值分別為1、5和11單位的硬幣,而希望找回總額為15單位的硬幣。按貪婪算法,應找1個11單位面值的硬幣和4個1單位面值的硬幣,共找回5個硬幣。但最優的解應是3個5單位面值的硬幣。
問題實例
1.裝箱問題
問題描述:裝箱問題可簡述如下:設有編號為0、1、…、n-1的n種物品,體積分別為v0、v1、…、vn-1。將這n種物品裝到容量都為V的若干箱子裡。約定這n種物品的體積均不超過V,即對於0≤i<n,有0<vi≤V。不同的裝箱方案所需要的箱子數目可能不同。裝箱問題要求使裝盡這n種物品的箱子數要少。
若考察將n種物品的集合分劃成n個或小於n個物品的所有子集,最優解就可以找到。但所有可能劃分的總數太大。對適當大的n,找出所有可能的劃分要花費的時間是無法承受的。為此,對裝箱問題採用非常簡單的近似算法,即貪婪法。該算法依次將物品放到它第一個能放進去的箱子中,該算法雖不能保證找到最優解,但還是能找到非常好的解。不失一般性,設n件物品的體積是按從大到小排好序的,即有v0≥v1≥…≥vn-1。如不滿足上述要求,只要先對這n件物品按它們的體積從大到小排序,然後按排序結果對物品重新編號即可。裝箱算法簡單描述如下:
{
輸 入 箱 子 的 容 積 ;
輸 入 物 品 種 數 n ;
按 體 積 從 大 到 小 順 序 , 輸 入 各 物 品 的 體 積 ;
預 置 已 用 箱 子 鏈 為 空 ;
預 置 已 用 箱 子 計 數 器 box_count 為 0 ;
for(i=0;i
{
從 已 用 的 第 一 只 箱 子 開 始 順 序 尋 找 能 放 入 物 品 i 的 箱 子 j ;
if ( 已 用 箱 子 都 不 能 再 放 物 品 i )
{
另 用 一 個 箱 子 , 並 將 物 品 i 放 入 該 箱 子 ;
box_count++;
}
else
將 物 品 i 放 入 箱 子 j ;
}
}
上述算法能求出需要的箱子數box_count,並能求出各箱子所裝物品。下面的例子說明該算法不一定能找到最優解,設有6種物品,它們的體積分別為:60、45、35、20、20和20單位體積,箱子的容積為100個單位體積。按上述算法計算,需三隻箱子,各箱子所裝物品分別為:第一隻箱子裝物品1、3;第二隻箱子裝物品2、4、5;第三隻箱子裝物品6。而最優解為兩隻箱子,分別裝物品1、4、5和2、3、6。若每隻箱子所裝物品用鍊表來表示,鍊表首結點指針存於一個結構中,結構記錄尚剩餘的空間量和該箱子所裝物品鍊表的首指針。另將全部箱子的信息也構成鍊表。以下是按以上算法編寫的程式。
程式:
# include
# include
typedef struct ELE
{
int VNO ;
struct ele*link ;
}
ELE ;
typedef struct hnode
{
int remainder ;
ELE*head ;
Struct hnode*next ;
}
HNODE ;
void main()
{
int n,i,box_count,box_volume,*a ;
HNODE*box_h,*box_t,*j ;
ELE*p,*q ;
Printf(“ 輸 入 箱 子 容 積 \ n ”);
Scanf(“%d ”,&box_volume);
Printf(“ 輸 入 物 品 種 數 \ n ”);
Scanf(“%d ”,&n);
A=(int*)malloc(sizeof(int)*n);
Printf(“ 請 按 體 積 從 大 到 小 順 序 輸 入 各 物 品 的 體 積 : ”);
For(i=0 ;
ivno=i ;
for(j=box_h;j!=NULL;j=j->next)
if(j->remainder>=a)break ;
if(j==NULL)
{
j=(HNODE*)malloc(sizeof(HNODE));
j->remainder=box_volume-a ;
j->head=NULL ;
if(box_h==NULL)box_h=box_t=j ;
else box_t=boix_t->next=j ;
j->next=NULL ;
box_count++;
}
else j->remainder-=a ;
for(q=j->next;q!=NULL&&q->link!=NULL;q=q->link);
if(q==NULL)
{
p->link=j->head ;
j->head=p ;
}
else
{
p->link=NULL ;
q->link=p ;
}
}
printf(“ 共 使 用 了%d 只 箱 子 ” , box_count);
printf(“ 各 箱 子 裝 物 品 情 況 如 下 : ”);
for(j=box_h,i=1;j!=NULL;j=j->next,i++)
{
printf(“ 第%2 d 只 箱 子 , 還 剩 余 容 積%4 d , 所 裝 物 品 有 ; \ n ”,I,j->remainder);
for(p=j->head;p!=NULL;p=p->link)
printf(“%4 d ”,p->vno+1);
printf(“ \ n ”);
}
}
2.馬的遍歷
問題描述:在8×8方格的棋盤上,從任意指定的方格出發,為馬尋找一條走遍棋盤每一格並且只經過一次的一條路徑。馬在某個方格,可以在一步內到達的不同位置最多有8個,如圖所示。如用二維數組board[ ][ ]表示棋盤,其元素記錄馬經過該位置時的步驟號。另對馬的8種可能走法(稱為著法)設定一個順序,如當前位置在棋盤的(i,j)方格,下一個可能的位置依次為(i+2,j+1)、(i+1,j+2)、(i-1,j+2)、(i-2,j+1)、(i-2,j-1)、(i-1,j-2)、(i+1,j-2)、(i+2,j-1),實際可以走的位置盡限於還未走過的和不越出邊界的那些位置。為便於程式的同意處理,可以引入兩個數組,分別存儲各種可能走法對當前位置的縱橫增量。
4 3
5 2
馬
6 1
7 0
對於本題,一般可以採用回溯法,這裡採用Warnsdoff策略求解,這也是一種貪婪法,其選擇下一出口的貪婪標準是在那些允許走的位置中,選擇出口最少的那個位置。如馬的當前位置(i,j)只有三個出口,他們是位置(i+2,j+1)、(i-2,j+1)和(i-1,j-2),如分別走到這些位置,這三個位置又分別會有不同的出口,假定這三個位置的出口個數分別為4、2、3,則程式就選擇讓馬走向(i-2,j+1)位置。由於程式採用的是一種貪婪法,整個找解過程是一直向前,沒有回溯,所以能非常快地找到解。但是,對於某些開始位置,實際上有解,而該算法不能找到解。對於找不到解的情況,程式只要改變8種可能出口的選擇順序,就能找到解。改變出口選擇順序,就是改變有相同出口時的選擇標準。以下程式考慮到這種情況,引入變數start,用於控制8種可能著法的選擇順序。開始時為0,當不能找到解時,就讓start增1,重新找解。細節以下程式。
程式:
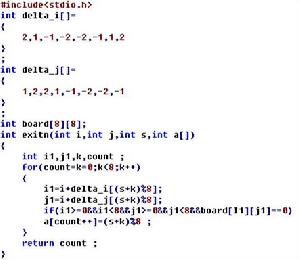 貪婪算
貪婪算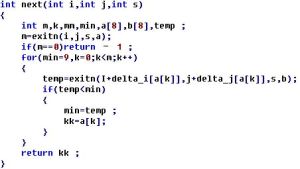 貪婪算
貪婪算 貪婪算
貪婪算