基本內容
幾何機率是十九世紀末新發展起來的一門學科,使很多機率問題的解決變得簡單而不用運用微積分的知識。然而,1899年,法國學者貝特朗提出了所謂“貝特朗悖論”(亦稱”貝特朗怪論“),矛頭直指幾何機率概念本身:
 貝特朗悖論
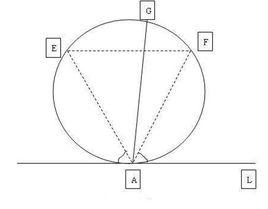
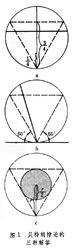
貝特朗悖論在一給定圓內所有的弦中任選一條弦,求該弦的長度長於圓的內接正三角形邊長的機率。該問題如圖一,有三種解決方法。
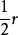 貝特朗悖論
貝特朗悖論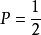 貝特朗悖論
貝特朗悖論1.如圖1第一幅圖,在垂直於三角形任意一邊的直徑上隨機取一個點,並通過該點做一條垂直於該直徑的弦,由圓內接正三角形的性質可得,在該點位於半徑中點的時候弦長度等於三角形的邊長度,當點離圓心的距離小於時弦長度大於三角形邊長。所以機率
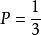 貝特朗悖論
貝特朗悖論2.如圖1第二幅圖,通過三角形任意一個頂點做圓的切線,因為等邊三角形內角為60°,所以左邊右邊的角都是60°。由該頂點做一條弦,弦的另一端在圓上任意一點。由圖可知弦與切線成60°角和120°角之間的時候弦長度大於三角形邊長。所以機率
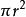 貝特朗悖論
貝特朗悖論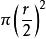 貝特朗悖論
貝特朗悖論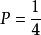 貝特朗悖論
貝特朗悖論3.如圖1第三幅圖,當弦的中點在陰影標記的圓內時,弦的長度大於三角形的邊長,而大圓的弦中點一定在圓內,大圓的面積是,小圓的面積是。所以機率
悖論分析
解法一:由於對稱性,可預先指定弦的方向。作垂直於此方向的直徑,只有交直徑於1/4 點與 3/4 點間的弦,其長才大於內接正三角形邊長。所有交點是等可能的,則所求機率為1/2 。此時假定弦的中心在直徑上均勻分布。
解法二:由於對稱性,可預先固定弦的一端。僅當弦與過此端點的切線的交角在60°~ 120° 之間,其長才合乎要求。所有方向是等可能的,則所求機率為1/3 。此時假定端點在圓周上均勻分布。
解法三: 弦被其中點位置唯一確定。只有當弦的中點落在半徑縮小了一半的同心圓內,其長才合乎要求。中點位置都是等可能的,則所求機率為1/4。此時假定弦長被其中心唯一確定。
這導致同一事件有不同機率,因此為悖論。
同一問題有三種不同答案,究其原因在於圓內“取弦”時規定尚不夠具體,不同的“等可能性假定”導致了不同的樣本空間,具體如下:其中“均勻分布”應理解為“等可能取點”。
解法一中假定弦的中點在直徑上均勻分布,直徑上的點組成樣本空間Ω1.
解法二中假定弦的另一端在圓周上均勻分布,圓周上的點組成樣本空間Ω2.
解法三中假定弦的中點在大圓內均勻分布,大圓內的點組成樣本空間Ω3.
可見,上述三個答案是針對三個不同樣本空間引起的,它們都是正確的,貝特朗悖論引起人們注意,在定義機率時要事先明確指出樣本空間是什麼。
術語使用
實際上,所謂“悖論”一點也不悖。這只是反映了選擇不同的坐標會導致不同的機率分配這一事實。至於哪一個分配是“正確”的,決定於事先確定的模型的如何套用或闡釋。
就以上悖論而言,造成這種現象的主要是在於條件的限制。若題目中出現“隨機”,“均勻分布”,“等可能”這些字眼,則對應著此悖論中1,2.3條的結果。
其他
貝特朗悖論在普通高中中模擬機率時會出現。一般第一種答案(即”1/3“)使用較為廣泛。
蘇教版(2004年初審通過)高中數學必修3第110頁有關於貝特朗悖論的介紹。
內容
伯特蘭給出了三個論證,全都是明顯有效的,但導致的結果都不相同。
隨機的弦,方法1
“隨機半徑”方法:選擇一個圓的半徑和半徑上的一點,再畫出通過此點並垂直半徑的弦。為了計算問題的機率,可以想像三角形會旋轉,使得其一邊會垂直於半徑。可觀察到,若選擇的點比三角形和半徑相交的點要接近圓的中心,則弦的長度會比三角形的邊較長。三角形的邊會平分半徑,因此隨機的弦會比三角形的邊較長的機率亦為二分之一。
隨機的弦,方法2
“隨機端點”方法:在圓周上隨機選給兩點,並畫出連線兩點的弦。為了計算問題中的機率,可以想像三角形會旋轉,使得其頂點會碰到弦端點中的一點。可觀察到,若另一個弦端點在弦會穿過三角形的一邊的弧上,則弦的長度會比三角形的邊較長。而弧的長度是圓周的三分之一,因此隨機的弦會比三角形的邊較長的機率亦為三分之一。
隨機的弦,方法3
“隨機中點”方法:選擇圓內的任意一點,並畫出以此點為中點的弦。可觀察到,若選擇的點落在半徑只有大圓的半徑的二分之一的同心圓之內,則弦的長度會比三角形的邊較長。小圓的面積是大圓的四分之一,因此隨機的弦會比三角形的邊較長的機率亦為四分之一。
1.隨機的弦,方法1
“隨機半徑”方法:選擇一個圓的半徑和半徑上的一點,再畫出通過此點並垂直半徑的弦。為了計算問題的機率,可以想像三角形會旋轉,使得其一邊會垂直於半徑。可觀察到,若選擇的點比三角形和半徑相交的點要接近圓的中心,則弦的長度會比三角形的邊較長。三角形的邊會平分半徑,因此隨機的弦會比三角形的邊較長的機率亦為二分之一。
2.隨機的弦,方法2
“隨機端點”方法:在圓周上隨機選給兩點,並畫出連線兩點的弦。為了計算問題中的機率,可以想像三角形會旋轉,使得其頂點會碰到弦端點中的一點。可觀察到,若另一個弦端點在弦會穿過三角形的一邊的弧上,則弦的長度會比三角形的邊較長。而弧的長度是圓周的三分之一,因此隨機的弦會比三角形的邊較長的機率亦為三分之一。
3.隨機的弦,方法3
“隨機中點”方法:選擇圓內的任意一點,並畫出以此點為中點的弦。可觀察到,若選擇的點落在半徑只有大圓的半徑的二分之一的同心圓之內,則弦的長度會比三角形的邊較長。小圓的面積是大圓的四分之一,因此隨機的弦會比三角形的邊較長的機率亦為四分之一。
4. 貝特朗悖論
貝特朗悖論上述方法可以如右圖示。每一個弦都可以被其中點唯一決定。上述三種方法會給出不同中點的分布。方法1和方法2會給出兩種不同不均勻的分布,而方法3則會給出一個均勻的方法。但另一方面,若直接看弦的分布,方法2的弦會看起來比較均勻,而方法1和方法3的弦則較不均勻。