簡介
變分被積函式是變分法中研究的主要函式。
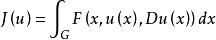 變分被積函式
變分被積函式形如 的泛函J(u)稱為變分積分,函式F(x,z,p)稱為變分被積函式或拉格朗日函式。
推廣
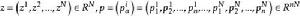 變分被積函式
變分被積函式Ω是R中的區域, 表示函式u對各自變數的偏導數,這裡u也可以是向量值函式。
當u是一元數量函式時,則用y表示,J(u)記為J(y),並稱為最簡變分積分。
變分法
變分法是17世紀末發展起來的一門數學分支,是處理函式的數學領域,和處理數的函式的普通微積分相對。它最終尋求的是極值函式:它們使得泛函取得極大或極小值。變分法起源於一些具體的物理學問題,最終由數學家研究解決。
有些曲線上的經典問題採用這種形式表達:一個例子是最速降線,在重力作用下一個粒子沿著該路徑可以在最短時間從點A到達不直接在它底下的一點B。在所有從A到B的曲線中必須極小化代表下降時間的表達式。
