動機
讓·勒雷當初為了研究代數拓撲學,而引入層的概念,從而面臨計算層上同調的問題。為此,勒雷發明了現稱勒雷譜序列的計算方法,它聯繫了一個層的上同調群與其正像的上同調群。
人們很快就發現:勒雷譜序列只是一個特例。譜序列還現身於纖維化等幾何問題;更抽象地說,對合成函子取導函子也會得到譜序列,稱為格羅滕迪克譜序列。雖然導範疇在理論層面提供了較簡煉的框架,譜序列仍是最有效的計算工具。
形式定義
 譜序列
譜序列 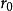 譜序列
譜序列 以下固定一個阿貝爾範疇,常見例子是一個環上的模範疇。 譜序列是一個非負整數 及下述資料:
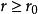 譜序列
譜序列 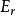 譜序列
譜序列 對所有整數 ,有範疇中的一個對象 。
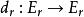 譜序列
譜序列 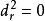 譜序列
譜序列 自同態 ,滿足 ,稱為 邊界映射或 微分。
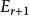 譜序列
譜序列 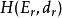 譜序列
譜序列 從 到 的同構。
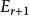 譜序列
譜序列 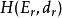 譜序列
譜序列 通常省去 與 的同構,而寫成等式。
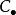 譜序列
譜序列 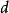 譜序列
譜序列 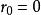 譜序列
譜序列 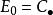 譜序列
譜序列 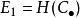 譜序列
譜序列 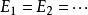 譜序列
譜序列 最基本的例子是鏈復形,它帶有一個微分 。取 ,並令 ,於是必有 ;這個新鏈復形上的微分只有一個自然的選擇,就是零映射。於是有 。綜之,我們得到一個鏈復形範疇上的譜序列:
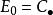 譜序列
譜序列  譜序列
譜序列 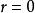 譜序列
譜序列 由於只有 時微分映射才可能非零,此序列在第一步後就不含任何新資訊。
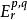 譜序列
譜序列  譜序列
譜序列 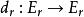 譜序列
譜序列 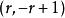 譜序列
譜序列 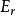 譜序列
譜序列 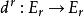 譜序列
譜序列 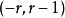 譜序列
譜序列 較常見的是雙分次模(或層)範疇上的譜序列,表作 ,此時的微分映射次數與 有關:對於上同調譜序列, 的次數是 。對於同調譜序列,通常將各項寫成 ,微分映射 的次數是 。
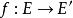 譜序列
譜序列 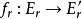 譜序列
譜序列 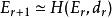 譜序列
譜序列 譜序列之間的態射 定義為一族態射 ,使之與同構 交換。譜序列對此構成了一個阿貝爾範疇。
正合偶
交換代數中大部分的譜序列來自鏈復形,而已知構造譜序列最有力的方法是 William Massey 的 正合偶。正合偶在代數拓撲學中很常見,此時對於許多譜序列,正合偶是唯一已知的構造法。事實上,正合偶可以用來構造所有已知的譜序列。
 譜序列
譜序列 同樣固定一個阿貝爾範疇(通常取一個環上的雙分次模) ,一個 正合偶是:
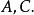 譜序列
譜序列 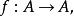 譜序列
譜序列 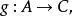 譜序列
譜序列 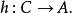 譜序列
譜序列 一對對象 三個態射: 使之滿足下述正合條件:
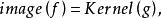 譜序列
譜序列 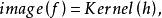 譜序列
譜序列 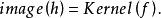 譜序列
譜序列 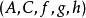 譜序列
譜序列 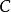 譜序列
譜序列 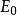 譜序列
譜序列  譜序列
譜序列 將這組資料簡記為 。正合偶通常以三角形表示。 對應到譜序列的 項,而 是一些輔助資料。
為了得到譜序列的後續項,以下將構造 導出偶。令:
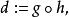 譜序列
譜序列 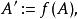 譜序列
譜序列 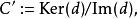 譜序列
譜序列 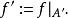 譜序列
譜序列 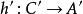 譜序列
譜序列 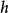 譜序列
譜序列 由導出。
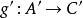 譜序列
譜序列  譜序列
譜序列 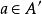 譜序列
譜序列 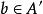 譜序列
譜序列 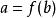 譜序列
譜序列 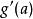 譜序列
譜序列 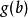 譜序列
譜序列 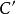 譜序列
譜序列 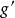 譜序列
譜序列 定義如下:若為某個環上的模範疇,對任一,存在使得,定義為在中的像。一般而言,可利用 Mitchell 嵌入定理構造態射。
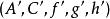 譜序列
譜序列 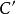 譜序列
譜序列 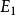 譜序列
譜序列 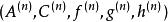 譜序列
譜序列 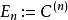 譜序列
譜序列 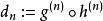 譜序列
譜序列 可以驗證構成正合偶。對應到譜序列的項。續行此法,可以得到一族正合偶。相應的譜序列定義為,。
收斂與退化
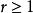 譜序列
譜序列 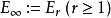 譜序列
譜序列 在第一個簡單的例子中,譜序列在後的微分映射皆為零,故不再改變。這時可定義該譜序列的 極限為。對於一般的譜序列,也往往存在一個極限,極限與各項的關係可說是譜序列的眾妙之門。
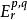 譜序列
譜序列 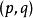 譜序列
譜序列 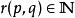 譜序列
譜序列 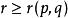 譜序列
譜序列 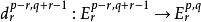 譜序列
譜序列 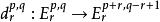 譜序列
譜序列 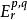 譜序列
譜序列 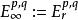 譜序列
譜序列  譜序列
譜序列 定義:若譜序列對每個都存在,使得當時,及皆為零,則稱之 極限項為(取充分大的)。最常見的例子是集中在第一象限的譜序列,此時極限項恆存在。
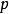 譜序列
譜序列 其中的指標指涉過濾結構。
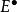 譜序列
譜序列 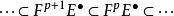 譜序列
譜序列 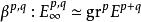 譜序列
譜序列 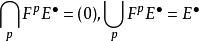 譜序列
譜序列 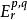 譜序列
譜序列 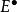 譜序列
譜序列 若存在對象、過濾結構,及一族同構,滿足(這種過濾稱為“正則過濾”),則稱 收斂到,通常表為下述符號:
 譜序列
譜序列 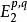 譜序列
譜序列 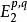 譜序列
譜序列 習慣上,人們也常將上式寫成,因為譜序列中最重要的頁往往是。
最簡單的收斂特例是 退化:
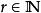 譜序列
譜序列 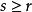 譜序列
譜序列 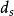 譜序列
譜序列  譜序列
譜序列 定義:固定,若對每個,微分映射都是零,則稱該譜序列在第頁退化。
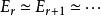 譜序列
譜序列 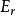 譜序列
譜序列 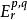 譜序列
譜序列 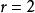 譜序列
譜序列 退化性保證了,此時即其極限。如果一個雙分次譜序列的非零項集中於某一條水平或垂直線上,則必在時退化。
