簡介
起源
“諧波”一詞起源於聲學。有關諧波的數學分析在18世紀和19世紀已經奠定了良好的基礎。傅立葉等人提出的諧波分析方法仍被廣泛套用。
電力系統的諧波問題早在20世紀20年代和30年代就引起了人們的注意。當時在德國，由於使用靜止汞弧變流器而造成了電壓、電流波形的畸變。1945年J.C.Read發表的有關變流器諧波的論文是早期有關諧波研究的經典論文。 到了50年代和60年代，由於高壓直流輸電技術的發展，發表了有關變流器引起電力系統諧波問題的大量論文。70年代以來，由於電力電子技術的飛速發展，各種電力電子裝置在電力系統、工業、交通及家庭中的套用日益廣泛，諧波所造成的危害也日趨嚴重。世界各國都對諧波問題予以充分的關注。國際上召開了多次有關諧波問題的學術會議，不少國家和國際學術組織都制定了限制電力系統諧波和用電設備諧波的標準和規定。
意義
諧波的危害十分嚴重——諧波使電能的生產、傳輸和利用的效率降低，使電氣設備過熱、產生振動和噪聲，並使絕緣老化，使用壽命縮短，甚至發生故障或燒毀。諧波可引起電力系統局部並聯諧振或串聯諧振，使諧波含量放大，造成電容器等設備燒毀。諧波還會引起繼電保護和自動裝置誤動作，使電能計量出現混亂。對於電力系統外部，諧波對通信設備和電子設備會產生嚴重干擾。
諧波危害
（1）諧波使公用電網中的元件產生了附加的諧波損耗，降低了發電、輸電及用電設備的效率，大量的3次諧波流過中性線時會使線路過熱甚至發生火災。
（2）諧波影響各種電氣設備的正常工作。諧波對電機的影響除引起附加損耗外，還會產生機械振動、噪聲和過電壓，使變壓器局部嚴重過熱。諧波使電容器、電纜等設備過熱、絕緣老化、壽命縮短，以至損壞。
（3）諧波會引起公用電網中局部的並聯諧振和串聯諧振，從而使諧波放大，這就使上述（1）和（2）的危害大大增加，甚至引起嚴重事故。
（4）諧波會導致繼電保護和自動裝置的誤動作，並會使電氣測量儀表計量不準確。
（5）諧波會對鄰近的通信系統產生干擾，輕者產生噪聲，降低通信質量；重者導致住處丟失，使通信系統無法正常工作。
分析方法
諧波分析滿足一定條件（Dirichlet條件）的、以T為周期的時間的周期函式f(t)，在連續點處，可用下述的三角函式的線性組合（傅立葉級數）來表示：
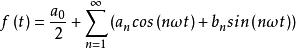諧波分析上式稱為f(t)的傅立葉級數，其中，ω=2π/T。
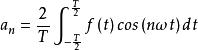諧波分析n為整數，n>=0。
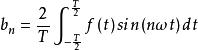諧波分析n為整數，n>=1。
在間斷點處，下式成立：
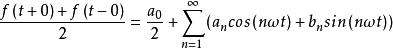諧波分析a0/2為信號f(t)的直流分量。
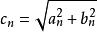諧波分析令
c1為基波幅值，cn為n次諧波的幅值。c1有時也稱1次諧波的幅值。a0/2有時也稱0次諧波的幅值。
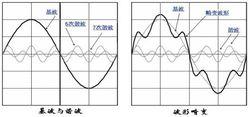
非正弦波里含有大量的諧波，不同的波形里含有不同的諧波成份。在倍頻器、變頻器里，就必須要進行諧波分析，分柝各次諧波的分布；在樂器、音響、放大器……也要分析諧波成份。
（1）奇次諧波，指頻率為基波頻率的3、5、7……倍的諧波；
（2）偶次諧波，指頻率是基波頻率的2、4、6……倍的諧波。
對f(t)=-f(t+T/2) 的函式(T為函式周期)，偶次諧波及直流分量為0；
對f(t)=f(t+T/2) 的函式(T為函式周期)， 奇次諧波為0。
測量方法
諧波分析是信號處理的一種基本手段。在電力系統的諧波分析中，主要採用各種諧波分析儀分析電網電壓、電流信號的諧波，該類儀表的諧波分析次數一般在40次以下。
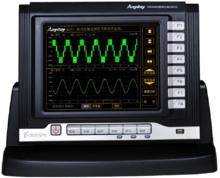諧波分析裝置及相關波形圖對於富含諧波的變頻器輸出的PWM波，其諧波主要集中在載波頻率的整數倍附近，當載波頻率高於基波頻率40倍時，採用上述諧波分析設備，其諧波含量近似等於零，不能滿足諧波分析的需要。
上述場合，當載波頻率固定時，諧波的頻率範圍相對固定，而所需分析的諧波次數，與基波頻率密切相關，基波頻率越低，需要分析的諧波次數越高。一般宜採用寬頻帶的，運算能力較強、存儲容量較大的變頻功率分析儀，根據需要，其諧波分析的次數可達數百甚至數千次。例如，當載波頻率為2kHz，基波頻率為50Hz時，其40次左右的諧波含量最大；當基波頻率為5Hz時，其400次左右的諧波含量最大，需要分析的諧波次數一般至少應達到2000次。
同時，選擇儀表的同時，還應選擇合適頻寬的感測器，因為感測器的頻寬將限制進入二次儀表的信號的有效頻寬。一般用選擇寬頻帶的電壓、電流感測器，如：變頻功率感測器。
凱塞窗插值FFT的電力諧波分析與套用
研究背景
高精度諧波分析對電能計量、諧波潮流計算、電力系統諧波補償與抑制等有重要意義。採用快速傅立葉變換(fastFouriertransform，FFT)算法進行諧波分析，非整周期截斷時產生頻譜泄漏和柵欄效應，影響諧波分析精度。針對FFT算法的不足，國內外學者提出了一系列加窗插值FFT算法。V.K.Jain等提出基於矩形窗的插值算法，可有效提高計算精度。此後，Hanning窗、Blackman-Harris窗、Rife-Vincent(I)窗、Nuttall窗和矩形卷積窗等被提出並被運用到FFT諧波分析中。基於餘弦組合窗的插值FFT算法、基於矩形窗的多譜線插值算法和採用多項式擬合的雙譜線插值方法等高精度插值FFT算法相繼被提出，提高了諧波分析精度。
採用矩形窗、三角窗等基本窗函式和廣義餘弦窗函式對信號加權，對於動態信號分析效果受到窗函式固定旁瓣性能的制約。Kaiser窗可定義一組可調的窗函式，其主瓣能量和旁瓣能量的比例近乎最大，且可自由選擇主瓣寬度和旁瓣高度之間的比重。研究對信號在整周期截斷和非整周期截斷時的頻譜進行分析，討論Kaiser窗的頻譜特性，提出基於Kaiser窗插值FFT的電力諧波分析算法，建立奇次、偶次諧波求解的數學模型和實用的插值修正公式，推導信號基波與各次諧波頻率、幅值和初相角計算式，採用包含21次諧波的動態信號仿真和三相諧波電能表套用實踐進一步證明研究方法的有效性和準確性。
實際套用
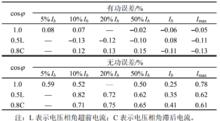表1 基波功率誤差基於本文提出的基於Kaiser窗插值FFT的電力諧波分析方法設計的三相多功能諧波電能表研製成功後，在湖南省電力公司計量中心進行了大量的試驗與測試檢驗。
實驗選擇基波功率疊加15次諧波功率為例。其中，基波電壓為220V，基波電流為1.5A。基波電壓疊加諧波電壓： U3=10%， U5=9%， U7=7%， U9=5%， U11=3%， U13=2%， U15=1%。基波電流疊加諧波電流： I3=20%， I5=15%， I7=12%， I9=10%， I11=8%， I13=7%， I15=5%，各次諧波相位差均為20°。標準源採用為JCD4060三相精密諧波源。
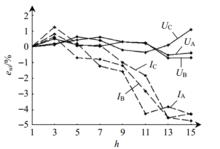圖1 各次諧波電壓與諧波電流誤差曲線圖表1給出比差角差校正後的基波功率誤差數據。圖1、2分別給出比差角差校正後ABC三相各次諧波電壓與諧波電流的誤差數據、基波功率因數cosϕ分別為1.0與0.5L時各次諧波相位的誤差數據。
由表1和圖1、2可知，測量準確度達到基波有功的相對誤差≤0.2%，基波無功的相對誤差≤1%，各次諧波電壓的相對誤差≤2%，各次諧波電流的相對誤差≤5%，諧波相位測量的絕對誤差≤5°，滿足A類諧波測量儀器標準GB/T14549—1993。
研究結論
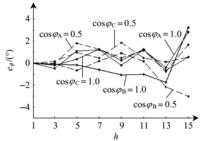圖2 各次諧波相位誤差曲線圖採用矩形、三角窗等基本窗函式和廣義餘弦窗函式對信號加權可減少非整數周期截斷造成的頻譜泄漏和柵欄效應影響，但其效果受到窗函式固定旁瓣性能的制約。Kaiser窗可定義一組可調的窗函式，自由選擇主瓣與旁瓣衰減之間的比重，因此能全面反映主瓣與旁瓣衰減之間的交換關係。本文根據Kaiser窗良好的頻譜泄漏抑制特性，結合FFT進行電力諧波分析，提出了基於Kaiser窗插值FFT算法，對包含21次諧波的動態信號仿真和三相多功能諧波電能表實際套用表明，採用本文提出的基於Kaiser窗插值FFT電力諧波分析方法，具有較高的計算精度，且設計靈活、實用價值高，據此實現的三相多功能諧波電能表準確度達0.2S級，2~21次諧波分析滿足GB/T14549—1993的A類諧波測量儀器要求。
