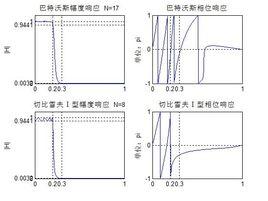
討論
 衝激不變法
衝激不變法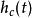 衝激不變法
衝激不變法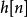 衝激不變法
衝激不變法以 為採樣周期對連續時間系統的衝激回響 採樣得到了離散時間系統的衝激回響 。
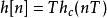 衝激不變法
衝激不變法因此,該系統的頻率回響為
 衝激不變法
衝激不變法 衝激不變法
衝激不變法 衝激不變法
衝激不變法如果連續時間濾波器是大致是帶限的(即當 時 ),則每次採樣的頻率低於 π(即奈奎斯特頻率低於1/(2 T) Hz)的離散時間系統的頻率回響就會大致為連續時間系統的頻率回響:
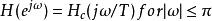 衝激不變法
衝激不變法與雙線性變換比較
注意到會出現混疊,包含有奈奎斯特頻率以下與超過該頻率連續時間濾波器的非零的回響混疊。雙線性變換使用不同的映射方法,將連續系統能夠達到無限頻率的頻率回響,映射到在離散時間系統中至多能達到奈奎斯特頻率的範圍,避免了衝激不變法線性地對頻率映射產生的循環混疊,從而可以替代衝激不變法。
系統函式中極點的效應
 衝激不變法
衝激不變法若連續極點位於,系統函式可以用部分分式展開寫作
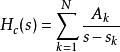 衝激不變法
衝激不變法因此,使用拉普拉斯逆變換,得到衝激回響為
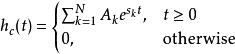 衝激不變法
衝激不變法對應的離散時間系統的衝激回響定義如下
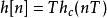 衝激不變法
衝激不變法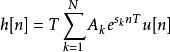 衝激不變法
衝激不變法對離散時間衝激回響進行Z變換得到下面的離散時間系統函式
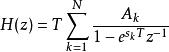 衝激不變法
衝激不變法於是連續時間系統函式的極點被搬移到z = e處的極點。零點則不會這樣簡單地映射過去。
零極點
如果系統函式既有零點也有極點,可以用相同方式映射,但結果不再是衝激不變的結果:離散時間衝激回響不是簡單地與連續時間衝激回響相等。這種方法名為匹配Z變換方法,或叫做零極點映射。對於全極點濾波器,兩種方法是等價的。
穩定性和因果性
由於連續時間系統 s = s 處的極點轉換到離散時間系統 z = exp( sT) 處的極點, s 左半平面的極點就會映射到 z 平面的單位圓內部;所以若連續時間濾波器是因果穩定的,則離散時間濾波器也會時因果穩定的。
修正公式
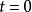 衝激不變法
衝激不變法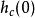 衝激不變法
衝激不變法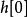 衝激不變法
衝激不變法當一個因果的連續時間衝激回響在處不連續時,上述表達式不一致。這是因為應道貢獻一半的值給。
修正為:
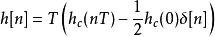 衝激不變法
衝激不變法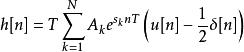 衝激不變法
衝激不變法對離散時間衝激回響進行Z變換得到下面的離散時間系統函式
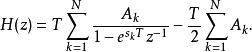 衝激不變法
衝激不變法