基本介紹
在拉丁方試驗設計中，有時根據試驗的要求，需要所用的拉丁方具有一些特殊的性質。例如，在把一塊農田分成若干縱橫小塊作試驗且根據一個拉丁方來安排試驗時，相鄰二小塊的安排之間彼此是有影響的，因而希望每一對可能的安排在所用的拉丁方的相鄰位置上出現一次。又如，養雞場關於飼料對雞的長勢的試驗且採用一個拉丁方來安排試驗時，接連使用的二種飼料彼此是有影響的，因而也希望每兩種不同飼料在所用的拉丁方中都能以不同的次序接連出現一次，這就引出了一類特殊的拉丁方，下面給出正式的定義。
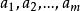行完備拉丁方定義1 設A=(a)是集S={ }上的一個m階拉丁方，如果S的每一個有序相異元素偶都在A的行中至少一次出現為相鄰(依有序對中的順序)的一對，則稱A是一個 行完備拉丁方，又稱為 水平完備拉丁方。如果在上面的定義中把“行”換為“列”，則稱A是一個 列完備拉丁方，又稱為 豎直完備拉丁 方。如果A既是行完備拉丁方，又是列完備拉丁方，則稱為一個 完 備拉丁方。
一個元的相鄰元根據其位置可以叫做右鄰元、左鄰元、上鄰元、下鄰元。
相關性質定理
由以上定義，有
引理1 在定義1中作下述更動，並不影響A的行完備性：
把“S的每一個有序相異元素偶都在A的行中至少一次出現為相鄰的一對”改為“S的每一個有序相異元素偶都在A的行中至多一次出現為相鄰的一對”，或改為“S的每一個有序相異元素偶都在A的行中恰好一次出現為相鄰的一對”。
證明S的有序相異元素偶的個數為
m(m-1)， (1)
A的每一行的有序相鄰元素偶的個數是m-1，A的諸行的相鄰元素偶的個數是m(m-1)，這與(1)相同，因此，S的每一相異元素偶在A的諸行中至少出現一次為相鄰元素的充要條件是，S的每一相異元素偶在A的諸行中恰好出現一次為相鄰元素，也是S的每一相異元素偶在A的諸行中至多出現一次為相鄰元素。證畢。
對於列完備拉丁方有類似的結果。
系 在引理1中把“行”換為“列”，引理的結論仍成立。
引理2 對一個拉丁方施行行換序並不改變它是否為行完備拉丁方，對一個拉丁方施行列換序並不改變它是否為列完備拉丁方。
證明 這是定義1的直接推論。
值得一提的是，對一個拉丁方施行列換序卻可能改變該拉丁方是否為行完備的這一性質。例如由下面的定理1可知
行完備拉丁方是一個完備拉丁方，若把它的頭二列交換，得
行完備拉丁方這雖然仍是一個列完備拉丁方(由引理2)，但卻不再是一個行完備拉丁方，因為有序元素偶(1，0)在第一和第四行中都出現為相鄰的元素偶。
設A是集[1，3]上的一個三階拉丁方，如果A的第一列上元1的右鄰元是2，則該列上元2的右鄰元必是3，元3的右鄰元必是1；因而第一列上元2的右鄰元必是3，元3的右鄰元必是1，元1的右鄰元必是2。這樣一來，有序元素偶(1，2)在A的諸行中出現了兩次，如果A的第一列上元1的右鄰元是3，則該列上元2的右鄰元必是1，元3的右鄰元必是2；因而第二列上元3的右鄰元必是2，元1的右鄰元必是3，元2的右鄰元必是1，這樣一來，有序元素偶(1，3)在A的諸行中出現了兩次，所以A不是行完備的。類似的推理可知A不是列完備的。這就是說，既不存在行完備也不存在列完備的三階拉丁方。
另一方面，下面的定理指出了構造偶數階完備拉丁方的一個一般性方法。
定理1(Williams) 設m=2l是個正偶數，設A是一個m×m矩陣，其第一行為：
0，1，2l-1，2，2l-2，3，2l-3，…，l-1，l+1，l， (2)
其它每一行是上一行諸元分別加1後取最小非負剩餘(mod m)而得，那么A是一個行完備拉丁方。如果經行換序把A的第一列諸元變成(2)的順序，那么此時的結果拉丁方是完備的。
由定義1還可推得完備拉丁方的下述性質。
定理2 設A是m元集S上的一個m階完備拉丁方，那么，對S中的任一元s，它在A中的右鄰元所組成的集就是S\{s}，這也是s的左鄰元所組成的集，s的上鄰元所組成的集，s的下鄰元所組成的集。
