有限群
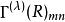舒爾正交關係
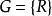舒爾正交關係
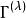舒爾正交關係 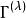舒爾正交關係令 是一個 |G| 階（即 G 有 |G| 個元素）有限群 ，的一個不可約矩陣表示 的矩陣元素。因為可以證明任何有限群的不可約矩陣表示等價於一個酉表示，我們假設 是酉的：
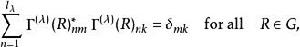舒爾正交關係
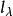舒爾正交關係 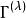舒爾正交關係這裡 是表示 的（有限）維數。正交關係，只對不可約表示的矩陣元素成立，是
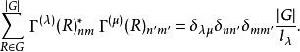舒爾正交關係
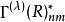舒爾正交關係 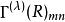舒爾正交關係
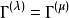舒爾正交關係
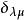舒爾正交關係 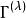舒爾正交關係
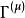舒爾正交關係 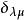舒爾正交關係
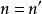舒爾正交關係
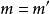舒爾正交關係這裡 是 的復共軛，求和遍及 G 的所有元素。如果兩個矩陣是在同一個不可約表示 ，則克羅內克函式 是單位，如果 與 不等價則 為零。其他兩個克羅內克函式則要求行與列的指標必須相等（ 和 ）才能得到一個非零的結果。這個定義也叫做廣義正交定理。
每個群有一個單位表示（所有群元素映為實數 1），這顯然是一個不可約表示。舒爾正交關係馬上給出
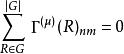舒爾正交關係
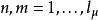舒爾正交關係 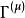舒爾正交關係對 ，此式對任何不等於單位表示的不可約表示 成立。
例子
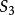舒爾正交關係
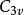舒爾正交關係 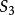舒爾正交關係
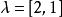舒爾正交關係 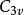舒爾正交關係
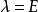舒爾正交關係三個對象的 3! 個置換組成一個 6 階群，通常記作 （對稱群）。這個群同構於點群 ，由三重旋轉軸以及三個鉛直鏡面平面組成。這個群有一個二維不可約表示（l = 2）。在 情形，通常將這個不可約表示利用楊氏表（楊氏矩陣）記作 而在 情形通常寫成 。在兩種情形不可約表示都由如下六個實矩陣組成，每個代表一個群元素
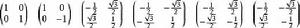舒爾正交關係元素 (1,1) 的正規化為：
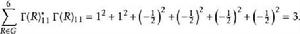舒爾正交關係同樣可以證明其它矩陣元素 (2,2)、(1,2) 與 (2,1) 的正規化。元素 (1,1) 與 (2,2) 的正交性：
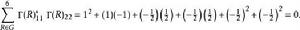舒爾正交關係類似的關係對元素 (1,1) 與 (1,2) 的正交性成立，如是等等。容易驗證此例中所有對應矩陣元素之和為零，因為給定表示與恆等表示的正交性。
直接推論
矩陣的跡是對角矩陣元素之和，
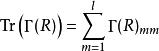舒爾正交關係
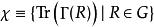舒爾正交關係
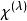舒爾正交關係所有跡的集合 是一個表示的特徵標。通常將一個不可約表示中矩陣的跡寫成
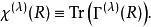舒爾正交關係利用這種記號我們可寫出多個特徵標公式：
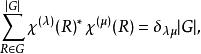舒爾正交關係這可以用來檢驗一個表示是否是可約的（這些公式說明在任意特徵標表中一行是正交向量）。以及
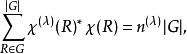舒爾正交關係 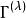舒爾正交關係
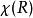舒爾正交關係
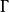舒爾正交關係這幫助我們確認不可約表示 在具有特徵標 的可約表示 中包含的次數。
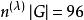舒爾正交關係
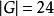舒爾正交關係 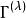舒爾正交關係 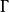舒爾正交關係
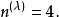舒爾正交關係例如，如果 ，這個群的階是 ，則 在給定“可約”表示 中包含的次數是
緊群
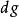舒爾正交關係
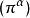舒爾正交關係
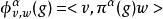舒爾正交關係
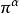舒爾正交關係
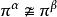舒爾正交關係有限群的正交關係推廣為緊群（包含緊李群，比如 SO(3)）本質上是簡單的：只要將在群上的求和換成在群上的積分。每個緊群G 有惟一一個雙不變哈爾測度，使得群的體積是 1。將這個測度記成 。設 是G的不可約表示的一個完備集合，設 是表示 的矩陣係數。正交關係可以敘述為兩部分 1) 如果 ，則：
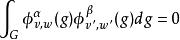舒爾正交關係
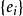舒爾正交關係 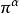舒爾正交關係2)如果 是表示空間 的一個正交規範基，則：
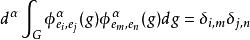舒爾正交關係
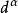舒爾正交關係 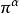舒爾正交關係這裡 是 的維數。這些正交關係以及所有表示的維數有限是彼得-外爾定理的推論。
例子
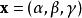舒爾正交關係
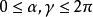舒爾正交關係
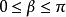舒爾正交關係一個三參數群的例子是矩陣群 SO(3)，有所有 3×3 正交矩陣組成。這個群的一個可能的參數化是利用歐拉角： 。界限是 以及 。
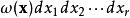舒爾正交關係
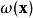舒爾正交關係體積元素 的計算不僅取決於參數的選取，也取決於最終結果，即加權函式（測度） 的解析形式。
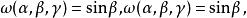舒爾正交關係
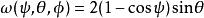舒爾正交關係
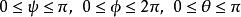舒爾正交關係例如，SO(3) 的歐拉角參數化給出權重 而 n, ψ 參數化給出權重t ，其中 。
可以證明一個緊李群的不可約表示是有限維的並可選成酉的：
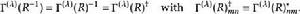舒爾正交關係簡記成：
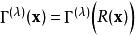舒爾正交關係正交關係具有形式：
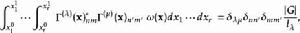舒爾正交關係群的體積是：
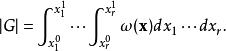舒爾正交關係
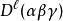舒爾正交關係
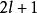舒爾正交關係我們注意到 SO(3) 的不可約表示是維格納D-矩陣（Wigner D-matrix） ，它們的維數是 ，故：
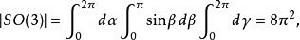舒爾正交關係他們滿足：
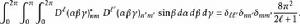舒爾正交關係