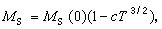自旋
在量子力學中, 自旋(英語:Spin)是粒子所具有的內稟性質,其運算規則類似於經典力學的角動量,並因此產生一個磁場。雖然有時會與經典力學中的自轉(例如行星公轉時同時進行的自轉)相類比,但實際上本質是迥異的。經典概念中的自轉,是物體對於其質心的旋轉,比如地球每日的自轉是順著一個通過地心的極軸所作的轉動。
首先對基本粒子提出自轉與相應角動量概念的是1925年由拉爾夫·克羅尼希、喬治·烏倫貝克與山繆·古德斯密特三人所開創。他們在處理電子的磁場理論時,把電子想像一個帶電的球體,自轉因而產生磁場。後來在量子力學中,透過理論以及實驗驗證發現基本粒子可視為是不可分割的點粒子,所以物體自轉無法直接套用到自旋角動量上來,因此僅能將自旋視為一種內稟性質,為粒子與生俱來帶有的一種角動量,並且其量值是量子化的,無法被改變(但自旋角動量的指向可以透過操作來改變)。
自旋對原子尺度的系統格外重要,諸如單一原子、質子、電子甚至是光子,都帶有正半奇數(1/2、3/2等等)或含零正整數(0、1、2)的自旋;半整數自旋的粒子被稱為費米子(如電子),整數的則稱為玻色子(如光子)。複合粒子也帶有自旋,其由組成粒子(可能是基本粒子)之自旋透過加法所得;例如質子的自旋可以從夸克自旋得到。
概論
自旋角動量是系統的一個可觀測量,它在空間中的三個分量和軌道角動量一樣滿足相同的對易關係。每個粒子都具有特有的自旋。粒子自旋角動量遵從角動量的普遍規律,p=[J(J+1)]h,此為自旋角動量量子數 ,J = 0,1 / 2,1,3/2,……。自旋為半奇數的粒子稱為費米子,服從費米-狄拉克統計;自旋為0或整數的粒子稱為玻色子,服從玻色-愛因斯坦統計。複合粒子的自旋是其內部各組成部分之間相對軌道角動量和各組成部分自旋的矢量和,即按量子力學中角動量相加法則求和。已發現的粒子中,自旋為整數的,最大自旋為4;自旋為半奇數的,最大自旋為3/2。
自旋是微觀粒子的一種性質,沒有經典對應,是一種全新的內稟自由度。自旋為半奇數的物質粒子服從泡利不相容原理。
概述
正如固體中相互作用的原子體系由於各種激發作用引起的集體運動,稱為點陣波(彈性波)或聲子一樣。早期,自旋波的概念曾用來精確解釋低溫下鐵磁體飽和磁化強度m隨溫度上升而下降的規律。由大量具有未抵消自旋的原子組成的鐵磁體,在T=0K時,由於交換作用所有自旋平行排列(完全有序); 當T>0K時,熱激發使鐵磁體中出現部分自旋的反向,而自旋間的相互作用使反向的自旋不固定在某些原子上,而在相鄰間的原子間傳播,也就是在自旋體系中傳播,形成自旋的集體運動。可以套用波動或準粒子來描述這種集體運動,分別稱為自旋波或磁振子。在不考慮自旋波之間相互作用的條件下,理論計算得到低溫下鐵磁體的飽和磁化強度隨溫度變化的較為精確的關係為: M(T)=C*T^(3/2)
這個規律為許多實驗所證實,並成為確定交換積分的主要實驗方法之一。在將自旋波看成準粒子的磁振子體系時,這些磁振子具有能量及動量。是相應的自旋波的(角)頻率,是其波矢,h=2是普朗克常數。序磁性體的自旋體系具有不同頻率和不同波矢 k的自旋波或不同能量和不同動量的磁振子。 由這些自旋波或磁振子分別組成自旋波譜或稱磁振子譜。自旋波的頻率與波矢或波數的函式關係稱為自旋波譜或頻散關係,在││很大的情形下,對於鐵磁體,對於反鐵磁體。
實驗方法
研究自旋波的實驗方法是利用自旋波與其他物理現象或因素的相互作用,例如磁共振方法、光散射方法和中子散射方法等。
自旋波除上述的熱激發外,還有其他的激發方法。例如,在鐵磁共振中,在均勻恆定磁場作用下,利用均勻的高頻磁場可激發=0的自旋波(即一致進動),亦可在薄膜中激發一定波數的自旋波駐波,稱為自旋波共振;利用非均勻的高頻磁場可激發0的自旋波(即非一致進動),大的自旋波稱為交換波;小的自旋波稱為靜磁波;當 很小以至其波長與樣品線度相當時稱為靜磁模。在高功率鐵磁共振中,當微波功率超過某臨界值時,由於一致進動與自旋波的耦合,某種自旋波可被激發。此外利用光子或中子與磁振子的非彈性散射也可激發自旋波。
研究意義
自旋波的研究對於基礎研究和實際套用都有重要意義。例如:自旋波的熱激發是決定若干基本磁性隨溫度變化的重要因素;由材料中各種不均勻性引起的=0和0的自旋波之間的散射是決定鐵磁共振線寬的重要弛豫機制;利用鐵氧體中激發和傳播的靜磁波可製成多種在微波技術中有用的靜磁波器件(如延遲線、濾波器、信噪比增強器等)。
自旋波函式
波函式是量子力學描寫微觀系統狀態 (又稱量子態或態) 的函式。是量子力學基本原理之一,也是量子力學中最基本最重要的量。在經典力學中,用質點的位置和動量(或速度) 來描寫巨觀質點的運動狀態,當坐標和動量確定之後,質點的其他力學量,如能量等也就隨之確定了。
自旋波函式是描述原子在自旋時系統狀態的波函式。
波函式
波函式是量子力學描寫微觀系統狀態 (又稱量子態或態) 的函式。是量子力學基本原理之一,也是量子力學中最基本最重要的量。在經典力學中,用質點的位置和動量(或速度) 來描寫巨觀質點的運動狀態,當坐標和動量確定之後,質點的其他力學量,如能量等也就隨之確定了。量子力學中描寫狀態的方式則不同。由於微觀粒子有波粒二象性,粒子的位置和動量不能同時有確定值,因而質點運動狀態的經典描述方式不再適用,代之以波函式來描寫微觀系統的狀態。波函式的物理意義和基本性質歸納起來是: (1) 如果不考慮粒子的自旋,波函式是坐標r和時間t的複函數,用符號ψ(r,t)表示。就坐標變數而言,獨立變數的數目等於微觀系統自由度數。例如,對於單粒子系統,獨立變數數目為3; 對於N個粒子系統,獨立變數數為3N。考慮微觀粒子的自旋後描寫狀態的波函式除了有位置和時間變數外,還應有自旋變數sz,這時波函式應表為ψ(r,s2,t)。(2) 對波函式的物理意義,玻恩首先提出了與實驗相符的統計解釋: 波函式模的平方給出粒子在空間一點出現的機率。因此波函式所表示的波和機械波、電磁波不同,它不是某種振動的傳播,而是代表一種機率分布。所以這種波也常被稱之為機率波。如單粒子系統處於由波函式ψ(r,t)所描寫的狀態,則|ψ(r,t)|2dr代表時刻t、空間r點附近dV體積內找到粒子的機率。如果描寫微觀系統狀態的波函式已知,則系統在該狀態下的各種力學量如坐標r、動量P、角動量L等的平均值或取值的機率可由波函式得出。就是說通過波函式可以得到系統相應狀態下的一切物理性質。顯然系統的狀態不同則相應的波函式也不同。(3) 波函式隨時間變化所遵從的規律是薛丁格方程。處於具體條件下的微觀系統的波函式,可由相應的薛丁格方程解出。(4)波函式ψ(r,t)不單要滿足薛丁格方程,還必須滿足以下條件: 波函式在變數變化的全部區域內必須滿足連續、單值、有限條件和歸一化條件: *(r,t)ψ(r,t)=1,這些條件稱為波函式的標準條件 。[3]