定義
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣自相關矩陣、自協方差矩陣、互相關矩陣以及互協方差矩陣他們都是用來描述隨機變數分布情況的工具 ,它們都與兩個向量的外積有關,因而需要首先定義兩個向量 和 的外積:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣兩個列向量 和 的外積給出一個m*n的矩陣,定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣其中, 與 均為行向量。
自相關矩陣或者自協方差矩陣都可以通過隨機向量之間的外積的數學期望來分別定義。
自相關矩陣與自協方差矩陣
自相關矩陣
自相關矩陣定義為隨機向量與自身的外積的數學期望:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣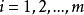 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣其中, 是隨機變數 的自相關係數,下標 ,
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣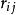 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣而 是隨機向量 和 的互相關係數,定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣顯然,自相關矩陣是復共軛對稱的,即為Hermitian矩陣。
自協方差矩陣
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣首先定義由各隨機向量均值構成的向量 ,則隨機向量 構成的協方差矩陣記為 ,定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣其中, 是隨機變數 的方差,即
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣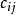 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣是隨機變數 與 的協方差,即
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣通過公式可以知道,自協方差矩陣也是Hermitian矩陣。自協方差矩陣也被稱為方差矩陣,用符號Var(x)表示。
自相關矩陣與自協方差矩陣的關係
自相關矩陣與自協方差矩陣存在如下關係:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣互相關矩陣與互協方差矩陣
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣通過自相關矩陣和自協方差矩陣的推廣,可以得到隨機向量 與 的互相關矩陣,定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣而互協方差矩陣則定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣其中, 為隨機變數 與 的互相關,而 則為他們的互協方差。
互相關矩陣與互協方差矩陣的關係
互相關矩陣與互協方差矩陣存在如下關係:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣當隨機向量 與 的維數不同時,他們的互相關矩陣和互協方差矩陣為非方陣,當他們的維數相同時,他們的互相關矩陣與互協方差矩陣為方陣,但仍不為復共軛對稱矩陣。
性質
協方差矩陣與互協方差矩陣由如下的性質:
(1)自協方差矩陣是復共軛轉置對稱的;
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣(2)線性組合向量 的自協方差矩陣 ;
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣(3)互協方差矩陣不是復共軛轉置對稱的,但是滿足 ;
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣(4) ;
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣(5)若隨機向量 與 具有相同的維數,則
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣(6) ;
引申
相關係數
自,互協方差矩陣主要用於描述矩陣各行,列向量之間的相關程度,但由於其元素是自,互協方差函式的絕對大小,有的時候在衡量相關度的時候並不準確,因而需要引入相關係數的概念,定義為:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣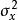 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣其中, 是隨機變數 與 的互協方差, 與 則表示 與 的方差。由Caucht-Schwartz不等式可以知道 。相關係數 給出了隨機向量 與 的相關程度,接近於0說明兩個向量的相似度越小,越接近於1說明兩個向量的相似度越大。
套用
自協方差矩陣的套用
 套用圖
套用圖儘管自協方差矩陣很簡單,可它卻是很多領域裡的非常有力的工具。例如,在數字圖像處理中,雖然圖像不一定是方陣,無法使用特徵值分解還原,但是圖像的自協方差矩陣必定是個實對稱矩陣,因而它能導出一個變換矩陣(導出過程可參考相關資料),這個矩陣能使數據完全去相關(decorrelation),從而能夠提取圖像中物體的特徵(人臉識別等套用)。從不同的角度看,也就是說能夠找出一組最佳的基以緊湊的方式來表達數據(用於數據壓縮)。這個方法在統計學中被稱為主成分分析(principal components analysis),在圖像處理中稱為Karhunen-Loève 變換(KL-變換)。
相關係數的套用
由於相關係數可以分析數據之間的相關性,因而也可以用於分析圖像的局部特徵,例如,有如下的圖像:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣可以求出這個圖像的自協方差矩陣和相關係數矩陣,自協方差矩陣如下所示:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣相關係數矩陣如下:
 相關矩陣與協方差矩陣
相關矩陣與協方差矩陣由自協方差矩陣圖可以看出,原圖的i列像素(50<i<100)與j列像素(50<j<100)的互協方差很大,即顏色變化很大,其他列之間的互協方差都很小,說明顏色變化也很小。而通過相關係數矩陣可以知道,原圖的i列像素(50<i<100)與j列像素(50<j<100)的相關係數很大,即很相似,且根據自協方差矩陣可以知道他們的顏色變化都很大。原圖的i列像素(200<i<250)與j列像素(0<j<50,200<j<250)的相關係數很大,即很相似,且顏色變化都很小。

