互協方差函式

互協方差函式(cross-covariance functions )，是反映兩個隨機向量 X 與 Y 相似關係的重要數量特徵，也稱為“互相關”，通常用於通過與已知信號做比較從來尋找未知信號的特點。

簡介

在統計學中， 互協方差函式表示兩個隨機向量 X與 Y之間的協方差cov( X, Y)，以區別於隨機向量 X的“協方差”即 X的各個標量元素之間的協方差矩陣。

在信號處理領域， 互協方差函式是兩個信號 (資訊理論)之間相似性的度量，它也稱為“互相關”。互協方差函式通常用於通過與已知信號做比較從來尋找未知信號的特點。它是信號之間相對於時間的函式，有時也稱為滑動點積，在模式識別與密碼分析學中都有套用。

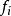互協方差函式

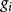互協方差函式

離散函式與的 互協方差函式定義為

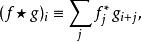互協方差函式

互協方差函式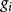

互協方差函式

其中累計和是在一個合適的整數上進行計算，星號表示是共軛複數。連續函式 f(x) 與的互協方差定義為

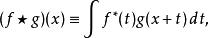互協方差函式

其中積分在合適的 t上進行。 互協方差本質上類似於兩個函式的卷積。

特性

因為

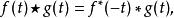互協方差函式

如果 f 或者 g 是偶函式，互協方差與卷積發生關係，

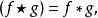互協方差函式

並且

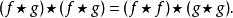互協方差函式

相關知識

•卷積

•相關性

•自協方差