聯合子區間法預測蘋果糖度
 圖1
圖1由於糖度是一個反映多種物質綜合作用的指標,因此用一個單獨的狹小子區間(即使有所擴張)來預測蘋果的糖度是不可行的。但同時,這一結果也提示了以較少波數點來獲得較高預測精度的另一種區間選取方法,即將同一次區間劃分中精度較高的幾個局部模型所在的區間聯合起來共同預測蘋果糖度(稱其為聯合子區間法)。圖1分別列出了將光譜劃分為10,11,…,20個子區間後,各最優聯合模型的建模區間,從表中可以看出,參加建立聯合最優模型的波數點數目都減少了一半以上,其中,波數點數目減少最多的聯合最優模型產生於將整個光譜區域劃分為19個子區間時,該模型建立於第1、5、6、7、8、11、12號子區間之上,只利用了553個波數點。
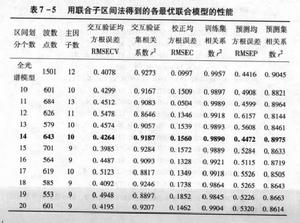 圖2
圖2圖2所示為各最優聯合模型的性能,從表中可以看出,採用多個子區間聯合建模後,糖度偏最小二乘模型的校正性能都較建立於單一子區間上的模型有所改善,它們的互動驗證均方根誤差RMSECV值都降到了0.55以下,比最優局部模型(基於區間“14—4”的模型)的RMSECV值下降了26%以上,相關係數r 也有了明顯的提高。特別是將光譜劃分為15個子區間時,利用其中的第1、4、5、6、7、9、10號等7個子區間聯合建立的糖度模型(為方便敘述,將其簡稱為“15—7”模型),其對互動驗證集樣本的預測能力超過了全光譜模型,儘管提高不是太明顯,但最重要的是,該模型得到了很大的簡化:其實際採用的波數點個數為701個,比全光譜模型採用的波數點個數減少了一半以上;這701個波數點最終組合為9個主因子,比全光譜模型的主因子數減少了3。但從圖2中也可以發現,研究中所得到的11個聯合模型對外部樣本的預測能力都沒有得到提高,相反還有所下降,尤其是上述“15—7模型”,其預測能力的下降最為明顯。
從簡潔性、預測能力等方面來綜合評價,將全光譜劃分為14個子區間時,建立於第1、4、5、6、8、9號等6個子區間之上的模型是11個最優聯合模型中最佳的(見圖2中粗體行所示),該模型只利用了643個波數點,採納的主因子數為10,與全光譜模型相比,該模型的預測能力有所下降。
從上面的結果可以看出,將精度較高的幾個局部模型所在的子區間聯合起來建立一個糖度預測模型是可行的。但目前尚不能從理論上確定參加聯合建模的子區間數目 。
區間偏最小二乘法的算法
常規區間偏最小二乘法
常規區間偏最小二乘波長篩選法(iPLS)是由Lars Norgaard於2000年提出的一種波長篩選法,該法主要用於篩選偏最小二乘建模的波長區域,其算法步驟如下:
(1)對原始光譜進行預處理;
(2)在全光譜範圍內建立待測品質的偏最小二乘模型(這裡稱為全局偏最小二乘模型);
(3)將整個光譜區域劃分為多個等寬的子區間,假設為n個;
(4)在每個子區間上進行偏最小二乘回歸,建立待測品質的“局部回歸模型”,也就是可以得到n個局部回歸模型;
(5)以互動驗證時的均方根誤差RMSEC值為各模型的精度衡量標準,分別比較全光譜模型和各局部模型的精度,取精度最高的局部模型所在的子區間為人選區間;
(6)對入選的區間進行最佳化,即以(5)中選定的區間為中心,單向或雙向擴充波長區域,最終得到一個最佳的波長區間。
由於農產品是組成非常複雜的天然生物體,其內部指標並不是以某種純的化學成分存在,單獨的一個小區間是不能提供足夠的信息來預測農產品指標。聯合區間偏最小二乘法和後面的向前/向後區間偏最小二乘法就是在這種情況下提出來的。從理論上講,聯合幾個子區間建立的預測模型,精度將更高 。
聯合區間偏最小二乘法
聯合區間偏最小二乘法是建立在常規區間偏最小二乘法的基礎上的一種方法,它將同一次區間劃分中精度較高的幾個局部模型所在的子區間聯合起來,共同預測農產品品質指標(稱其為聯合子區間法)。實際套用表明,將精度較高的幾個局部模型所在的子區間聯合起來建立的預測模型是可行的。但目前尚不能從理論上確定參加聯合建模的子區間數目。
向前區間偏最小二乘篩選法的基本原理
向前閾值區間偏最小二乘篩選法(FiPLST)基於Lars NФrgaard的iPLS理論,同時引進了向前選擇變數法的思想,是一種“只進不出”的方法,其算法步驟如下:
(1)對原始光譜進行預處理;
(2)在全光譜範圍內建立待測品質的偏最小二乘模型(這裡稱為全局偏最小二乘模型);
(3)將整個光譜區域劃分為多個等寬的子區間,假設為n個;
(4)在每個子區間上進行偏最小二乘回歸,建立待測品質的“局部回歸模型”,也就是可以得到n個局部回歸模型;
(5)以互動驗證時的均方根誤差RMSECV值為各模型的精度衡量標準,分別比較全光譜模型和各局部模型的精度,取精度最高的局部模型所在的子區間為第一入選區間;
(6)將餘下的(n一1)個子區間逐一與第一入選子區間聯合,產生(n一1)組聯合區間,並在每一聯合區間上進行偏最小二乘回歸,得到(n一1)個聯合模型,選擇其中RMSECV值最低的模型所在的子區間為第二入選區間。這樣運行下去,直至餘下所有子區間都將進入聯合模型;
(7)考察第(6)步中每次聯合模型的RMSECV值,找出在所有模型中選出性能最佳者(RMSECV最小),其所對應的區間組合即為最佳組合。
向後區間偏最小二乘篩選法的基本原理
向後區間偏最小二乘法是一種“只出不進”的方法,其算法(1)、(2)、(3)與FiPLS法一樣;
(4)每次去掉1個子區間,在餘下(n一1)個聯合區間進行偏最小二乘回歸,得到n個聯合區間的回歸模型;
(5)以互動驗證時的均方根誤差RMSECV值為各模型的精度衡量標準,分別比較各聯合模型的精度,取精度最高的聯合模型時所去掉的子區間為第一去掉子區間;
(6)將餘下的(n一1)個子區間逐一去除一個子區間,產生(n一1)組聯合區間,並在每一聯合區間上進行偏最小二乘回歸,得到(n一1)個聯合模型,選擇其中RMSECV值最低的模型所對應去除的子區間為第二去除的區間。這樣運行下去,直至剩下一個子區間模型;
(7)與FiPLS法一樣。可以看出,向影向後區間偏最小二乘篩選法(FiPLS/BiPLS)採用的仍然是幾個子區間聯合建模的方法,但其區間的搜尋方法繼承了向前/向後選擇變數法“只進不出”/“只出不進”的特點,因此可以很方便地確定聯合模型的建模區間數。同時向前/向後區間偏最小二乘篩選法能在不同的區間劃分(即將光譜劃分為不同數目的子區間)中搜尋到最佳的聯合區間。從現有的套用實例來看,通過各種區間偏最小二乘法選取合適的光譜區間進行建模,可以減小建模運算時間,剔除噪聲過大的變數區域,使最終建立的農產品品質指標預測模型的預測能力更強,精度更高 。