耦合常數
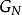 耦合常數的跑動
耦合常數的跑動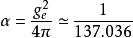 耦合常數的跑動
耦合常數的跑動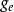 耦合常數的跑動
耦合常數的跑動 耦合常數的跑動
耦合常數的跑動在物理學中, 耦合常數決定了相互作用的強度。例如在牛頓萬有引力定律和愛因斯坦的廣義相對論中,牛頓常數 就是引力的耦合常數。在粒子物理中,耦合常數的數值常常通過精細結構常數來給出。例如電磁相互作用的精細結構常數為 , 其中 是電磁相互作用的耦合常數,它正比與電子電荷 。在日常使用時,耦合常數也經常和精細結構常數換用。
在拉格朗日系統中,拉格朗日量或哈密頓量可以分成動能部分和相互作用部分。耦合常數決定了決定了相互作用部分相對於動能部分的強度。在存在多種相互作用的情況下,耦合常數也決定著各個相互作用的相對強度。
在經典力學中,耦合常數的大小可以通過測量力的大小直接得到。歷史上牛頓常數是在牛頓死後71年後才由卡文迪什通過扭秤實驗測量得到。但在量子力學中由於量子漲落的存在,出現在拉格朗日量或哈密頓量中的耦合常數是無法直接通過測量得到的。而實驗中測量得到的耦合常數會隨著探測尺度的不同而不同,被稱為跑動的耦合常數。相應的,拉格朗日量中的耦合常數被稱為裸耦合常數。
如果一個物理系統的相互作用的耦合常數比較小,則它的解可以通過微擾論近似得到。微擾論在量子場論的計算中尤其重要。
基本相互作用
強、弱、電磁和引力四種基本相互作用中的耦合常數的大小大致如下:
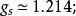 耦合常數的跑動
耦合常數的跑動強相互作用的耦合常數:
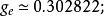 耦合常數的跑動
耦合常數的跑動電磁相互作用的耦合常數:
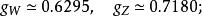 耦合常數的跑動
耦合常數的跑動弱相互作用的耦合常數:
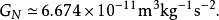 耦合常數的跑動
耦合常數的跑動引力相互作用的耦合常數:
弱耦合與微擾論
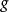 耦合常數的跑動
耦合常數的跑動 耦合常數的跑動
耦合常數的跑動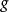 耦合常數的跑動
耦合常數的跑動如果一個問題中的耦合常數 遠小於單位一,則其稱為“弱耦合”的,此時問題的解 可以按照 的冪次(又叫做階數)展開表示為:
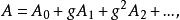 耦合常數的跑動
耦合常數的跑動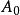 耦合常數的跑動
耦合常數的跑動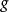 耦合常數的跑動
耦合常數的跑動其中, 為沒有相互作用時問題的解。這種方法稱為微擾論。在上述微擾展開中,越高階項的貢獻越小。因而可以在適當階做截斷,以滿足給定的精度要求。微擾論只有在弱耦合時才有用,因為若耦合常數 大於一,則越高階項的貢獻越大,任何有限階數的截斷都會帶來嚴重的誤差。
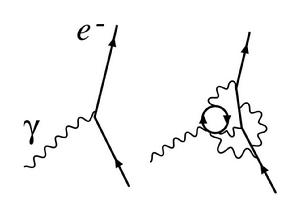
微擾論在量子場論中具有核心地位。量子場論中的微擾論計算一般是通過費曼圖和費曼規則來系統地組織實現的,因為費曼圖就是按照耦合常數的冪次畫出來的。電磁相互作用、弱相互作用在尋常尺度下都是弱耦合的相互作用。而強相互作用在短距離上(尺度遠小于飛米時)也是弱耦合的。
跑動的耦合常數
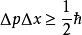 耦合常數的跑動
耦合常數的跑動在量子力學尤其是量子場論中,由於量子漲落效應的存在,相互作用頂點被虛粒子所修正,成為非定域性的相互作用頂點。因此,測得的耦合常數的大小與原拉格朗日量或哈密頓量中的裸耦合常數不同,且與測量的能量標度有關。後一點可以通過不確定關係, 來理解。測量使用的能量越高,測量儀器能夠分辨的尺度就越小。在小尺度下,將能看到更多的虛粒子的漲落。這種效應與電荷在介質中的極化效應是相似的。因而也被稱為真空極化。這種隨著能標的改變而改變的“耦合常數”被稱為 跑動的耦合常數。
β函式β(g) 描述了耦合常數隨能量標度μ變化的的情形,其定義如下:
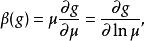 耦合常數的跑動
耦合常數的跑動其中μ為特定物理過程的能量標度。
若量子場論中的β函式為零,則此理論為共形場論。若在高能量下β函式為正,代表耦合常數隨著能標的增加而增加;若在高能量下β函式為負,則代表耦合常數隨著能標的增加減小,這種現象叫做 漸近自由。
量子電動力學和朗道奇點
根據微擾論,描寫電磁相互作用的量子電動力學的β函式為正,耦合效應會隨著能量增加而增強。量子電動力學在高能量時會變得高度耦合,甚至在某些有限時能量下,耦合係數似乎會變成無限大,此現象最早是由列夫·達維多維奇·郎道所發現,因此稱為郎道奇點。不過微擾論在強耦合情況下已經失效。而且達到朗道奇點所需的能標遠遠超過普朗克能標,而一般認為量子場論在普朗克能標左右已經不再適用。
量子色動力學和漸近自由
弗朗克·韋爾切克、休·波利策及戴維·格婁斯發現,描寫強相互作用的量子色動力學的β函式為負。因此量子色動力學的耦合在高能量時會降低。其發現者因此獲得2004年的諾貝爾物理獎。在一階近似下耦合係數大致可以表示為下式:
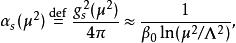 耦合常數的跑動
耦合常數的跑動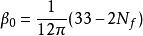 耦合常數的跑動
耦合常數的跑動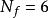 耦合常數的跑動
耦合常數的跑動其中 為一常數, 是夸克味的數目。這是最先由韋爾切克、波利策和格婁斯計算的。
相反的,耦合程度會隨著能量降低而增強,因此在低能量時耦合效應會變強。尤其是在能標Λ上由微擾論定義耦合常數開始出現發散,因此不能用微擾效應來求解。Λ稱為QCD尺度,其數值為
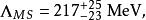 耦合常數的跑動
耦合常數的跑動大致對應於一飛米。
弦理論
弦理論下的耦合常數有明顯的不同點,弦耦合常數一方面意味著決定一根弦分裂的能力,另一方面則意味著弦理論的每一個微擾敘述和一個弦耦合常數有關,可是這些耦合常數不是事先定義、可調整及共適性的常數,而是動態的標量場,會依位置和時間改善,而其數值需動態決定。
相關條目
•耦合 (物理學)
•量子場論、量子電動力學及量子色動力學
•規範量子化、重整化及維度正則化
•精細結構常數
•重力耦合常數
•費米耦合常數