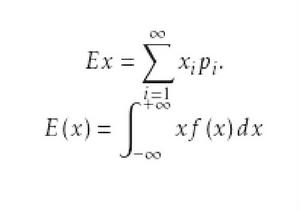基本介紹
總體均值又叫做總體的數學期望或簡稱期望,是描述隨機變數取值平均狀況的數字特徵 。
離散型隨機變數的總體均值
 總體均值
總體均值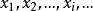 總體均值
總體均值設離散型隨機變數 的可能取值是 ,取這些值的相應機率為
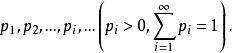 總體均值
總體均值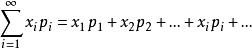 總體均值
總體均值 總體均值
總體均值若 絕對收斂,則 稱為隨機變數的總體均值。記作
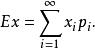 總體均值
總體均值連續型隨機變數的總體均值
 總體均值
總體均值 總體均值
總體均值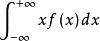 總體均值
總體均值 總體均值
總體均值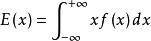 總體均值
總體均值設連續型隨機變數 的分布密度是 ,若積分 絕對收斂,則稱該積分為總體 的均值,記作 。
總體均值的基本性質
總體均值具有以下基本性質:
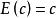 總體均值
總體均值①對任意常數c,均有 ;
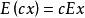 總體均值
總體均值② ,其中c為任意常數;
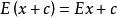 總體均值
總體均值③ ,其中c為任意常數;
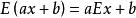 總體均值
總體均值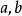 總體均值
總體均值④ ,其中 為任意常數;
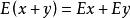 總體均值
總體均值⑤對於兩個隨機變數x和y,有 ;
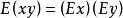 總體均值
總體均值⑥若兩個隨機變數x和y相互獨立,則有 。
基本性質⑤、⑥可以推廣到有限個的情況,這就是:n個隨機變數和的均值等於均值的和;n個隨機變數若相互獨立,則乘積的均值等於均值的乘積。這時n為有限整數且大於2 。
總體均值的點估計
 總體均值
總體均值 總體均值
總體均值 總體均值
總體均值參數估計就是以樣本統計量來估計總體參數,例如,用樣本平均數估計總體平均數,用樣本成數估計總體成數,等等。在參數估計中,用來估計總體參數 的樣本統計量 ,稱為 估計量。例如,樣本平均數、樣本成數、樣本方差等。用來估計總體參數時計算出來的估計量的具體數值 ,稱為 估計值。例如,要估計一個班級考試的平均分數,現從中抽取一個隨機樣本,經過計算得到樣本平均分數為80分,那么這個80分就是估計值。
參數估計的方法有 點估計和 區間估計。
點估計就是直接以樣本統計量作為總體參數的估計量,又稱為 定值估計。例如,以樣本平均數、樣本成數、樣本方差作為相應總體參數的估計量,即
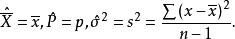 總體均值
總體均值總體均值的區間估計
方差已知時總體均值的區間估計
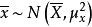 總體均值
總體均值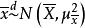 總體均值
總體均值若總體服從常態分配,則樣本均值 ;若總體不服從常態分配,但當樣本容量n足夠大時,則 。進一步可得 :
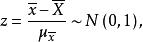 總體均值
總體均值 總體均值
總體均值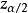 總體均值
總體均值給定顯著性水平 ,查標準常態分配表可得到臨界值 ,且滿足:
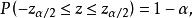 總體均值
總體均值 總體均值
總體均值則在置信水平 下總體均值的區間估計為
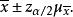 總體均值
總體均值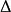 總體均值
總體均值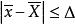 總體均值
總體均值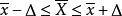 總體均值
總體均值 總體均值
總體均值反過來,設總體均值的抽樣允許誤差為 ,即 ,且區間估計 的置信水平為 ,則有
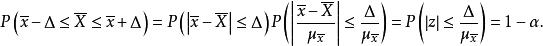 總體均值
總體均值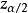 總體均值
總體均值 總體均值
總體均值 總體均值
總體均值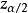 總體均值
總體均值 總體均值
總體均值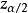 總體均值
總體均值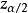 總體均值
總體均值臨界值 與置信水平 一一對應。給定一個置信水平 ,可以通過查 標準正態 分布表確定臨界值 。若置信水平提高,即區間估計的可靠程度增大,則 減小,即臨界值 增大。反之,若置信水平減小,則臨界值減小。臨界值 稱為機率度,用符號z表示,用以間接地衡量區間估計的機率大小。
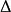 總體均值
總體均值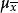 總體均值
總體均值易見,抽樣允許誤差 、抽樣平均誤差 和機率度z三者存在如下關係:
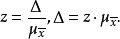 總體均值
總體均值 總體均值
總體均值給定置信水平 ,在重複抽樣條件下,總體均值的置信區間為
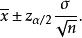 總體均值
總體均值在不重複抽樣條件下,總體均值的置信區間為
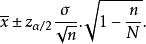 總體均值
總體均值方差未知時總體均值的區間估計
若總體服從常態分配但總體方差未知,則可用樣本標準差s代替總體標準差s構造統計量,即得
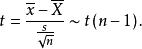 總體均值
總體均值 總體均值
總體均值給定置信水平 ,在重複抽樣條件下,總體均值的置信區間為
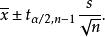 總體均值
總體均值類似地,在不重複抽樣條件下,總體均值的置信區間為
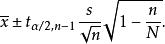 總體均值
總體均值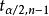 總體均值
總體均值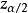 總體均值
總體均值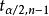 總體均值
總體均值查t分布表可得到臨界值 。在大樣本情況下,t分布近似於標準常態分配。所以,此時也可以用標準常態分配臨界值 代替 。