簡介
總體,又譯 母體。是指統計學中是指由許多有某種共同性質的事物組成的集合,會在此集合中選出樣本進行統計推斷,選取樣本的方式可能會用亂數或是其他抽樣方式。
例如要針對所有烏鴉的共有特性進行研究,總體是目前存在、以前曾經存在或是未來可能存在的所有烏鴉,此情形下,因為時間的限制、地域可取得性的限制、以及研究者的有限資源等,不可能觀測總體中的每一個,因此研究者會從總體中產生樣本,再由樣本的特性去了解總體的特性。
產生樣本的目的之一就是為了要知道總體的特性,包括:
 目標總體
目標總體1.總體均值,用 表示,若總體的數量是有限的,總體均值等於所有數值的算術平均數。
 目標總體
目標總體2.總體標準差,用 表示,基本定義如下:
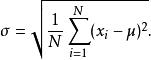 目標總體
目標總體子總體
總體的子集稱為子總體,若不同的子總體有不同的性質,則整個總體具有異質性,若將總體區分為不同的子總體,可以對整個總體的特質有較多的了解。例如某特定藥物可能對不同的的子總體有不同的影響,若在取樣時沒有取到該子總體,可能就忽略了這樣的影響。
區分子總體也有助於更精確的估計參數,例如考慮男性和女性是不同的子總體,可以針對人類身高的分布有更好的建模。
包括子總體的總體可以用混合模式建模,將各子總體的分布結合成整個總體的分布,不過即使子總體都可以用簡單的模型來表示,總體仍可能在用簡單模型來擬合時有很差的效果。例如有二個都是常態分配的子總體,兩者的標準差相同,但平均值不同,所得的總體分布會是峰度較低的常態分配,若兩者平均值的差距過大,甚至還會變成雙峰分布,而其標準差也可能會比原來子總體的要大。例如有二個都是常態分配的子總體,兩者的平均值相同,但標準差不同,會有峰度較高的常態分配。
相關條目
•抽樣
