定義
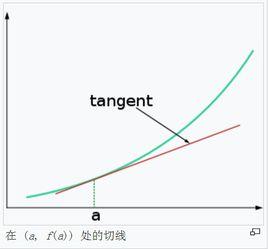
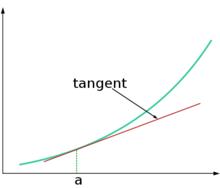 圖1.線性近似,切線近似
圖1.線性近似,切線近似所謂線性近似,也叫線性逼近,主要作用是把一個複雜的非線性函式用一個簡單的線性函式來表示。
假設一般函式上存在點(a, f(a)),當x接近a時,可以使用函式在a點的切線作為函式的近似線。函式L(x)≈f(a)+f'(a)(x-a)即稱為函式f在a點的 線性近似或 切線近似 。
例如,有一個實數變數的可導函式 f,根據 n=1的泰勒公式,
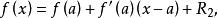 線性近似
線性近似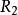 線性近似
線性近似其中 是餘數。捨去餘數就是線性近似:
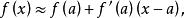 線性近似
線性近似當 x無限接近於 a的時候這個等式成立。
圖1的表示是 f在點 ( a, f( a)) 處的切線,因此這個過程也叫作 切線近似。
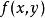 線性近似
線性近似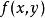 線性近似
線性近似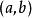 線性近似
線性近似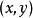 線性近似
線性近似我們也可以對以向量作為變數的向量函式作 線性近似,這時在該點的導數用雅可比矩陣代替 。例如,一個有實數變數的可導函式 ,可以用函式 在接近 的 點處的值來近似,
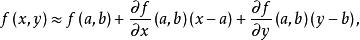 線性近似
線性近似 線性近似
線性近似 線性近似
線性近似方程右側是在點處的平面切線。
在更具普遍意義的巴拿赫空間上,
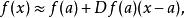 線性近似
線性近似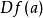 線性近似
線性近似 線性近似
線性近似 線性近似
線性近似其中 是函式 在 處的 Fréchet 導數。
示例
線性近似的方法在尋找函式近似值時有很大作用:
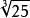 線性近似
線性近似例1.求 的值。
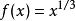 線性近似
線性近似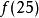 線性近似
線性近似1) 設函式 ,問題化為求 的值,
2)可以得到
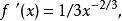 線性近似
線性近似3)根據 線性近似
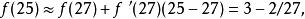 線性近似
線性近似4)結果 2.926 非常接近於實際值 2.924。
幾何意義
線性近似求解的是近似值,其幾何意義是在基點的切線近似於原函式的曲線 。
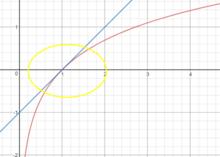 圖2.線性近似的幾何意義——切線
圖2.線性近似的幾何意義——切線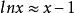 線性近似
線性近似以f(x)=lnx為例,根據公式,在x=1, ,曲線和切線如圖2所示:
在x=1點附近,曲線近似於直線,x越接近x,二者的近似度越高。在討論近似時,只有指定基點才有意義。這很容易理解,x越遠離x,曲線和直線的差距越大;同時,當基點不同時,切線的斜率也不同。
常用線性近似公式
x=0時,常用的線性近似值:
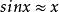 線性近似
線性近似1);
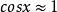 線性近似
線性近似2);
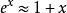 線性近似
線性近似3);
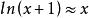 線性近似
線性近似4);
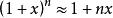 線性近似
線性近似5)。