線性映射矩陣

線性映射矩陣(matrix of a linear mapping)是一種特殊矩陣，指線性映射的數量表示。設σ是數域P上n維線性空間V到P上m維線性空間W的一個線性映射，v1，v2，…，vn是V的基，w1，w2，…，wm是W的基。若(σ(v1)，σ(v2)，…，σ(vn))=(w1，w2，…，wm)(aij)m×n，則矩陣(aij)稱為σ關於基偶(v1，v2，…，vn)，(w1，w2，…，wm)的矩陣。設V的基變換為(v1′，v2′，…，vn′)=(v1，v2，…，vn)R，W的基變換為(w1′，w2′，…，wm′)=(w1，w2，…，wm)Q，則線性映射σ關於基偶(v1′，v2′，…，vn′)，(w1′，w2′，…，wm′)的矩陣(aij′)與(aij)是等價的，即(aij′)=Q(aij)R.若W=V，則線性變換σ對基v1，v2，…，vn的矩陣(aij)與對基v1′，v2′，…，vn′的矩陣(aij′)是相似的，即(aij′)=R(aij)R，其中(v1′，v2′，…，vn′)=(v1，v2，…，vn)R 。

基本介紹

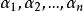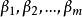線性映射矩陣

線性映射矩陣

線性映射矩陣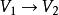

線性映射矩陣

設是V的一組基，是V的一組基。是的個線性映射，則

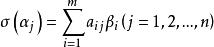線性映射矩陣

或寫成

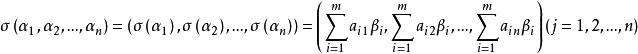線性映射矩陣

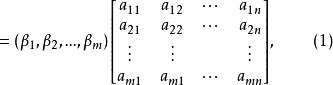線性映射矩陣

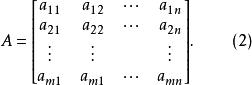線性映射矩陣

把它代入式（1）得

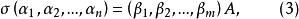線性映射矩陣

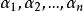線性映射矩陣

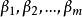線性映射矩陣

矩陣A稱為線性映射σ在基()與()下的 矩陣表示 。

有了線性映射(在一對基下)的矩陣表示現在可以解決V中向量α與它在V中的像之間的坐標關係。

設α∈V，故

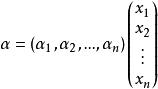線性映射矩陣

它的像σ(α)∈V，可寫成

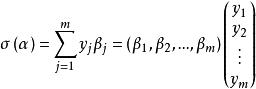線性映射矩陣

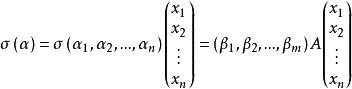線性映射矩陣

根據σ(α)坐標唯一性，得

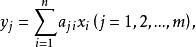線性映射矩陣

寫成矩陣形式

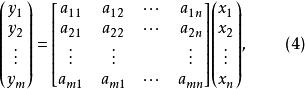線性映射矩陣

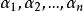線性映射矩陣

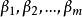線性映射矩陣

式(4)稱為線性映射在給定基()與()下向量坐標變換公式(原像與像的坐標關係) 。

相關定理

線性映射σ在給定基下的矩陣表示A是唯一的，它的逆問題就是下述定理 。

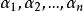線性映射矩陣

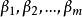線性映射矩陣

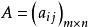線性映射矩陣

定理1 設V的基為，V的基為，已給m×n矩陣，則存在唯一的線性映射σ，它在這兩個基下的矩陣表示為A。

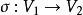線性映射矩陣

在指定了空間V和V的基之後，便可以求得線性映射在指定一對基下的矩陣表示。但是空間基是不唯一的，線性映射在不同對基下的矩陣表示之間有如下關係。

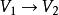線性映射矩陣

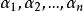線性映射矩陣

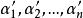線性映射矩陣

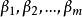線性映射矩陣

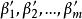線性映射矩陣

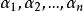線性映射矩陣

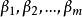線性映射矩陣

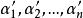線性映射矩陣

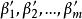線性映射矩陣

定理2 設σ是的一個線性映射，與是V的兩組基，其過渡矩陣為與是V的兩組基，其過渡矩陣為Q。線性映射σ在基與下的矩陣表示為A，在基與下的矩陣表示為B，則

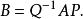線性映射矩陣