基礎知識
 線性插值
線性插值 線性插值
線性插值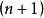 線性插值
線性插值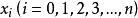 線性插值
線性插值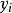 線性插值
線性插值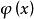 線性插值
線性插值已知函式 在區間 上 個互異點 上的函式值 ,若存在一簡單函式 ,使
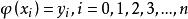 線性插值
線性插值並要求誤差
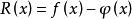 線性插值
線性插值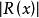 線性插值
線性插值 線性插值
線性插值的絕對值 在整個區間 上比較小。這樣的問題稱為插值問題。
其中
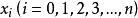 線性插值
線性插值:插值節點
 線性插值
線性插值:被插值函式
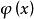 線性插值
線性插值:插值函式
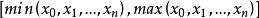 線性插值
線性插值:插值區間
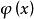 線性插值
線性插值 線性插值
線性插值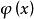 線性插值
線性插值 線性插值
線性插值如果在插值區間內部用 代替 則稱為內插;在插值區間以外,用 代替 則稱為外插。
簡介
線性插值是一種較為簡單的插值方法,其插值函式為一次多項式。線性插值,在各插值節點上插值的誤差為0 。
 線性插值
線性插值 線性插值
線性插值 線性插值
線性插值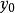 線性插值
線性插值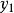 線性插值
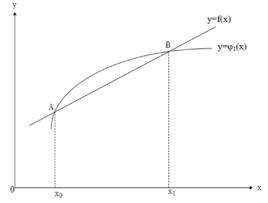
線性插值如概述圖中所示,設函式 在兩點 , 上的值分別為 , ,求多項式
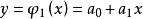 線性插值
線性插值使滿足
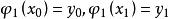 線性插值
線性插值由解析幾何可知
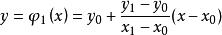 線性插值
線性插值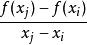 線性插值
線性插值 線性插值
線性插值 線性插值
線性插值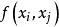 線性插值
線性插值稱 為 在 處的一階均差,記以 。於是,得
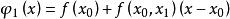 線性插值
線性插值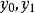 線性插值
線性插值如果按照 整理,則
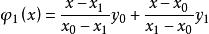 線性插值
線性插值以上插值多項式為一次多項式,這種插值稱為線性插值。
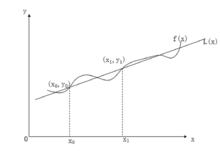
幾何意義
 線性插值
線性插值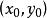 線性插值
線性插值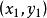 線性插值
線性插值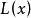 線性插值
線性插值 線性插值
線性插值線性插值的幾何意義如右圖所示,即為利用過點 和 的直線 來近似原函式 。
套用
1)線性插值在一定允許誤差下,可以近似代替原來函式;
2)在查詢各種數值表時,可通過線性插值來得到表中沒有的數值。