簡介
偏微分方程論
偏微分方程論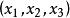
偏微分方程論
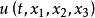偏微分方程論偏微分方程論是研究這類方程的一個數學分支學科，一般亦稱為偏微分方程。客觀世界的物理量一般可能表示成時間 與空間位置坐標 的函式 ，它的變化規律往往表現為它關於時間和空間坐標的各階變化率之間的關係，即函式u與 的各階偏導數之間的等式.
這樣一類包含未知函式及其偏導數的等式稱為偏微分方程。由幾個偏微分方程所構成的等式組(未知函式也可以是幾個)稱為偏微分方程組。偏微分方程或偏微分方程組中所含偏導數的最高階數稱為此方程或方程組的階。
發展
在微積分理論形成不久的18世紀，人們就研究用微分方程來描述物理問題，並針對具體的物理問題求解。人們最早研究的是弦的橫振動方程達朗貝爾(D'Alembert, J. 1e R.)最先得出它的通解;丹尼爾第一·伯努利 (Bernoulli , Daniel I)從弦的聲音是由基音和泛音疊加而成的觀點出發，認為方程的所有可能的解是的形狀，其中l是弦長；達朗貝爾、歐拉(Eider, L. ) 和拉格朗日(I,agrange , J. -L.)還研究了兩端固定的弦滿足初始條件的解，並對解的允許函式進行了激烈的爭論.歐拉和拉格朗日在流體力學的工作中，勒讓德(Legendre, A. -M.)與拉普拉斯((Laplace , P. -S.)在天體力學的工作中都研究了調和方程。在流體力學的論文中，柯西(Cauchy,A.)得到了現在所稱的柯西一黎曼方程組，歐拉得出了理想流體動力學方程組。
18世紀末，蒙日(Monge )開創了用幾何解釋偏微分方程的思想，對一階和二階非線性方程建立了完整的特徵理論。19世紀，傅立葉(Fourier)系統研究了熱傳導方程，闡述了把有界區間上初邊值問題的解表為三角級數或貝塞爾函式、勒讓德函式的級數的一般分離變數法，對初值問題通過積分變換得出了解的表達式.他的工作不僅使微分方程的發展邁出了重要的一步，而且使人們把函式的概念從單個解析表達式中解放出來，促進了函式論、級數理論的發展，引起了人們對數學的邏輯基礎的探討。同時，還出現了許多現在以首創者命名的方程、公式和解法。例如，引力場的泊松方程、泊松公式、格林公式、格林函式，解二階雙曲型方程的黎曼方法，粘性流體運動的納維一斯托克斯方程，柯西彈性力學方程組，電磁波的麥克斯韋方程組。這些成就對科學技術的發展起了巨大的推動作用，例如，麥克斯韋 (Maxwell , J. C.)預言電磁波以光速通過空間，斷言光是電磁現象，鼓舞了洛倫茲(Lorentz,H. A.)關於電子的學說和愛因斯坦(Einstein, A.)關於相對論的研究。柯西給出了第一個關於解的存在定理，開創了偏微分方程的現代理論.杜·布瓦一雷蒙(Du Bois-Reymond , P. D. G.)提出把二階線性偏微分方程分為橢圓、雙曲和拋物三種類型.到19世紀末，二階線性偏微分方程的一般理論已基本建立，偏微分方程或者稱數學物理方程這一學科開始形成. 20世紀30年代起，各種泛函分析方法陸續被套用於偏微分方程的研究。20世紀40年代，紹德爾 (Schauder , J. P.)所採用的先驗估計方法，不僅完滿地建立了一般二階線性橢圓型方程的古典解理論，而且為解決偏微分方程定解問題提供了非常有用的技巧。20世紀40年代末期出現的廣義函式與索伯列夫空間理論，為偏微分方程理論的進一步發展提供了基本的工具。20世紀50到60年代，一方面作為線性分型方程理論的擴展和深人，一般線性偏微分運算元理論得到了發展;另一方面，由於先驗估計的深人發展，擬線性橢圓和拋物方程理論有了重大的進展，擬線性雙曲方程(組)的間斷解的研究也有許多好的成果。
近二三十年進展較快，且在當前國際上有較多人研究的偏微分方程問題有:線上性問題方面，微分運算元的概念已先後推廣為擬微分運算元、傅立葉積分運算元和仿微分運算元，利用它們研究偏微分方程解的存在、解的光滑性、定解問題的惟一性、局部可解性、解的奇性傳播與反射等問題，都取得了很好的結果。微局部分析方法是新發展起來的重要工具，利用它不僅解決了線性方程的許多新問題，且被逐步推廣套用於處理非線性問題。在非線性問題方面，研究得較多的有擬線性與完全非線性橢圓及拋物方程、非線性雙曲方程、孤立波、自由邊界問題、反應擴散方程、多重解和分歧解等。研究中，不動點理論、拓撲度、變分方法(包括臨界點理論)、上(下)解方法、單調運算元理論、非線性半群、隱函式定理及變分不等式等方法和工具不斷發展並得到了新的套用.微分流形上的偏微分方程的研究也取得了許多深人的結果，微分幾何與偏微分方程的相互滲透成為一個重要的發展趨勢。
偏微分方程
偏微分方程論偏微分方程中常以 為未知數及偏微分，如下：
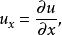偏微分方程論
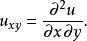偏微分方程論
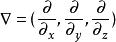偏微分方程論
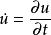偏微分方程論用於空間偏微分的梯度運運算元 ，和時間偏微分 。
常微分方程
常微分方程是本科數學專業的核心基礎課程，內容包括：微分方程建模、初等積分法、線性系統、常係數線性系統、若干振動問題、一般理論、定性理論初步。自微積分創立以來，人們就開始研究微分方程。從最初的初等求解技巧到今天日益發達的數值模擬技術，從早期對方向場的理解到今天關於微分方程定性理論、分岔理論的成熟知識體系，三百多年的歷史使這門數學分支不僅成為了數學學科中隊伍最大、綜合性最強的領域之一，而且成為數學以外學科最為關注的領域之一。也正是因為科技發展對於微分方程的要求越來越強烈，所以各個學校都在結合自身的特點，開展一些教學上的改革，在課堂上展開多種形式的教學，力圖使學生能夠深刻理解微分方程所要傳達的信息。
常微分方程課堂教學建設的主要內容，數學類各專業培養具有良好的數學基礎和數學思維能力，受到數學建模、計算機和數學軟體方面的基本訓練，在數學和數學套用方面受到良好的教育，具有較高的科學素養和較強的創新意識，具備科學研究、解決實際問題及軟體開發等方面的基本能力和較強的更新知識能力的綜合人才。常微分方程課程是繼數學分析、高等代數之後的一門重要基礎課程，為學習泛函分析、偏微分方程等後繼課程提供強有力支撐，也是套用性很強的一門課程，在實現數學、力學等專業培養目標中具有不可替代的重要作用。綜合考慮該課程的特點，以及與其他相關課程的銜接問題，明確課程定位，確立本課程的具體目標為：（1）強化理論基礎，服務後續課程；（2）強化建模思想和方法，鼓勵學生思考，提高動手能力，培養創新意識。為此，加強課堂建設，需要從以下幾方面入手 ：
1.把課堂知識模組化，突出重點加強難點
2.採取靈活的教學模式，提高課堂教學質量
3.教學形式與手段的多樣化，促進課堂教學
