定義
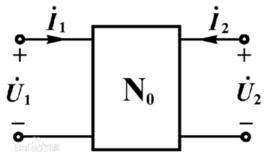
表示線性電網路的激勵與回響關係的一種函式。在內部不含獨立電源的電路的某一連線埠施加一個激勵e(t),在該激勵的作用下,電路中某零狀態回響r(t)經過拉普拉斯變換後的象函式R(s)與激勵的象函式E(s)之比即稱為網路函式 。
數學表達式為:H(s)=R(s)/E(s).
表示線性電網路的激勵與回響關係的一種函式。網路中的激勵、回響可以是電壓或電流,於是網路函式有4種類型:①激勵與回響均為電壓(流)時,網路函式是轉移電壓(流)比。②激勵是電壓、回響是電流時,網路函式稱為轉移導納。③激勵是電流、回響是電壓時,網路函式稱為轉移阻抗。④激勵電壓(流)和回響電流(壓)同在一個連線埠時,網路函式稱為驅動點導納(阻抗),又稱驅動點函式。對網路函式性質的研究是電網路理論中有重要意義的課題。網路綜合(研究滿足給定回響特性的網路設計方法)的理論便是在這一研究的基礎上建立起來的。
若輸入和輸出屬於同一連線埠,稱為驅動點函式,或策動點函式。若輸入和輸出屬於不同連線埠時,稱為轉移函式。
計算方法
網路函式的計算方法
正弦穩態電路的網路函式是以 ω為變數的兩個多項式之比,它取決於網路的結構和參數,與輸入的量值無關。
在已知網路相量模型的條件下,計算網路函式的基本方法是外加電源法:在輸入端外加一個電壓源或電流源,用正弦穩態分析的任一種方法求輸出相量的表達式,然後將輸出相量與輸入相量相比,求得相應的網路函式。對於二端元件組成的阻抗串並聯網路,也可用阻抗串並聯公式計算驅動點阻抗和導納,用分壓、分流公式計算轉移函式。
網路函式與頻率特性之間的關係
從H(jk)本身的物理概念、物理意義出發
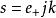 網路函式
網路函式網路函式H(s)是當激勵e(t)是單位衝激函式時零狀態回響H(t)的象函式,是衝激回響h(t)經過拉普拉斯變換後得到的變化式。當s=jk時相當於時相當於拉普拉斯變化式中的復變數中e=0,也就是收斂因子為1,那么當原時域函式h(t)乘以大小為1的收斂因子時,相當於沒有乘收斂因子一樣,此時的拉氏變換實際上為傅氏變換。可見H(jk)是原時域函式h(t)的傅氏變換。根據傅氏變換的物理意義可知,H(jk)是h(t)的頻譜函式,因而其模|H(jk)|稱為幅頻特性、其幅角稱為相頻特性 。
從頻域中激勵與回響之間的關係看
 網路函式
網路函式在頻域,H(jk)是激勵1(k)的回響。單位衝激函式的傅立葉變換為1(k),表明W(t)中含有無窮豐富的頻率成分,且各種頻率成分的相對大小均相同,W(t)的頻率也因此稱為白色頻譜,它是研究頻率特性的非常理想的激勵。輸入相對大小均為1的各種頻率的信號,那么輸出的回響中看看哪些頻率的信號受到抑制而減小,哪些頻率的信號可以通過或者放大,各種頻率的信號的相移為多少,這樣,就能說明H(jk)的模與k的關係反映了一個電路系統的幅頻特性、其幅角與k的關係反映了一個電路系統的相頻特性了 。
從時域中激勵與回響之間的關係看
當輸入一個頻率為k振幅為1的正弦激勵,輸出的穩態分量與輸入量是同頻率的,只是輸出穩態分量的振幅在輸入量的振幅的基礎上有一個大小為H(jk)的模的增益,相角有一個θ(k)的相移,由此可見:對於不同頻率k的激勵,對應有不同的|H(jk)|和θ(k),輸出的大小、相移也不相同,這就表明H(jk)反映了電路系統的頻率特性 。
以上三個方面的論述實際上是統一的。時域的單位衝激激勵W(t)由無窮多個幅值相同的不同頻率的無窮小信號合成,h(t)由無窮多個幅值不同的對應頻率的無窮小信號合成,即上述第二點。而W(t)和h(t)的頻譜分別為l(k)和H(jk),正說明各個不同頻率的無窮小信號通過系統後引起了大小的變化|H(jk)|和相位的變化θ(k),總變化為H(jk),此即上述第三點,這樣也就印證了網路函式H(s)在當s=jk就是頻譜函式,即第一點 。