多端網路

簡介

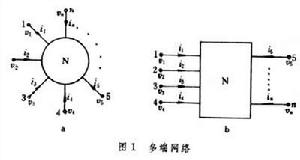
外伸端子數n等於或大於3的網路。它是隨著電路日趨複雜而出現的一種概念。許多用來組裝電路的元、器件和電工設備的電路模型是多端網路。如半導體三極體的電路模型是三端網路；單相電力變壓器的電路模型是四端網路；而當前已大量使用的積體電路則是端子更多的多端網路。多端網路理論中的二連線埠網路理論（見二連線埠網路）早已被廣泛地套用於電路分析和綜合。

約束關係

一

多端網路

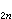個多端網路通常用圖1a或圖1b來表示。這是一種不顯示內部結構的黑箱子表示法。圖中端子上vk（K＝1,2,…,n）代表端子對參考點（圖上未標出）的電壓；ik(K=1,2,…,n)代表流入端子的電流。表達多端網路外部性能（簡稱外特性）的是存在於端子電壓與端子電流之間的約束關係。對於一個不含獨立電源且處於正弦穩態下的線性時不變多端網路，根據疊加定理，約束關係由方程組：夒1＝Y11妭1＋Y12妭2＋…＋Y1n妭n2＝Y21妭1＋Y22妭2＋…＋Y妭n……………………夒n＝Yn1妭1＋Y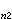妭2＋…＋Y妭n來描述。將此方程組寫成矩陣形式，則為：拵＝尯夳
式中 拵＝【夒1夒2…夒n】T 是以端子電流為分量的電流相量；夳＝【妭1妭2…妭n】T 是以端子電壓為分量的電壓相量；尯是以方程組中的諸係數Yij(i,j＝1,2,…,n)為元素的n×n方陣，即
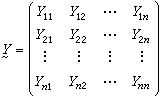
上述方程組稱為多端網路的外特性方程,而Yij 和尯 分別稱為多端網路的不定導納和不定導納矩陣。從方程組可得
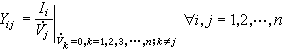
此式是不定導納的定義式。在多端網路內部連線方式已知的情況下，不定導納Yij可根據此式通過計算求出。
根據基爾霍夫電流定律(KCL)應有：夒n＝－(夒1＋夒2＋…＋夒)
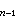再將此式與外特性方程相結合，可導出

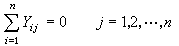多端網路

多端網路

還可證實
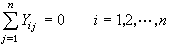
上述結果表明不定導納矩陣尯具有下列性質:①其任意一列的元素之和恆為零；②其任意一行的元素之和恆為零。由此可知,一個具有n個端子的多端網路的n2 個不定導納中只有(n-1)2 個獨立；尯 是奇異矩陣,其秩為n-1。

多連線埠網路

當多端網路的一對端子上的電流滿足從一端子流入的電流恆等於從另一端子流出的電流的條件時，這對端子便構成該網路的一個連線埠。上述條件稱為連線埠電流約束條件,簡稱連線埠條件。一個多端網路,若其端子能兩兩成對形成連線埠，則此網路又稱多口網路。顯然，多口網路是滿足連線埠電流約束條件的多端網路。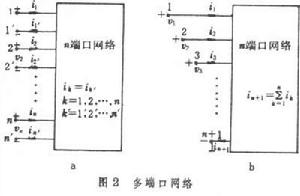

圖2a上的網路是一個n連線埠網路,其端子數為2n，端子對(1,1┡)，(2,2┡),…,(n,n┡)是網路的n個連線埠；圖2b上的網路是另一個n 連線埠網路，其端子數為n+1,端子對(1,n+1),(2,n+1)，…,(n,n+1)是網路的n個連線埠。顯而易見,將圖2a所示n連線埠網路的端子1┡，2┡，…，n┡一起接地，便可得到圖2b所示的n連線埠網路。
多連線埠網路的參數方程　對於不含獨立電源的線性時不變多連線埠網路，利用疊加定理可以寫出：
①含短路導納參數的方程
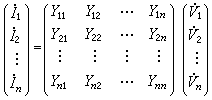
式中右端的n×n方陣是多連線埠網路的短路導納矩陣；矩陣元素
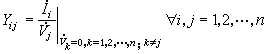
下標相同,即i=j的元素稱為短路策動點導納；下標不同，即i≠j的元素稱為短路轉移導納。短路導納是這兩種導納的總稱。
②含開路阻抗參數的方程
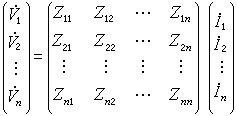
式中右端的n×n方陣是多連線埠網路的開路阻抗矩陣；矩陣元素
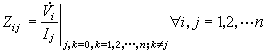
下標相同,即i=j的元素稱為開路策動點阻抗；下標不同，即i≠j的元素稱為開路轉移阻抗。開路阻抗是這兩種阻抗的總稱。
③含混合參數的方程
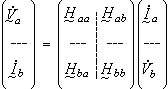
式中夳a=【妭1妭2…妭k】T 和拵a＝【夒1夒2…夒k】T 分別是前K個連線埠電壓和連線埠電流組成的相量;拵b=【夒k+1夒k+2…夒n】T 和夳b＝【妭k+1妭k+2…妭n】T 分別是後 n-K個連線埠電流和連線埠電壓組成的相量；右端的係數矩陣是多連線埠網路的混合參數矩陣，此矩陣中的子矩陣
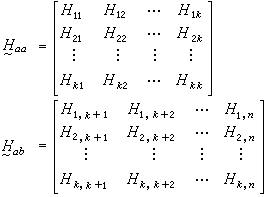
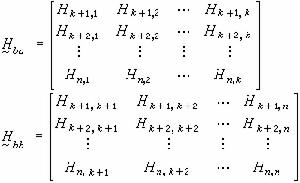
而且媨aa中的元素具有阻抗的量綱;媨bb中的元素具有導納的量綱；至於媨ab和媨ba中的元素,則都是無量綱的複數。
多連線埠網路理論已成為分析電路的有力工具。對含有非線性元件的電路，用此理論進行分析會收到較好的效果。

參考書目

肖達川編著：《電路分析》,科學出版社,北京，1984。