維納核估計
正文
用泛函級數模型逼近非線性系統的動態過程,又稱白噪聲估計方法。1887年V.沃爾泰拉引用一致收斂的泛函級數來逼近連續函式,這就是著名的沃爾泰拉級數。可以用沃爾泰拉級數來逼近一個非線性系統的輸入輸出關係。但是由於沃爾泰拉級數的核不是正交的,在估計這些核時不能簡單地通過輸入激勵和系統的回響來得到結果。1958年R.維納建立一組正交核:
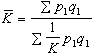
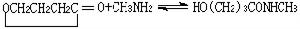
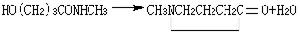
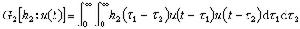
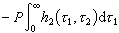
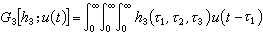
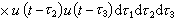
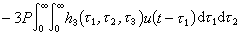
利用Gm的正交性和正態白噪聲的性質可以通過不同的途徑比較方便地得到hm的估計。最常用的是互相關方法,也就是利用輸入和輸出的互相關函式來估計hm。
前幾階核的估計是:
h0=E 【y(t)】
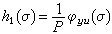
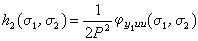
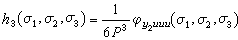
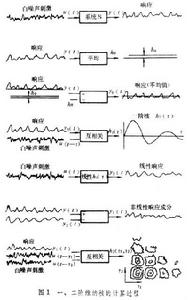 圖1是典型的一、二階核計算方法。圖中是在白噪聲刺激(輸入)下系統的回響曲線y(t);回響曲線的零階核h0(常數),即y(t)的期望值;y(t)減去期望值得到的零均值回響y0;y0與白噪聲的互相關函式h1(τ),即一階核;白噪聲的刺激下一階核的線性回響y2(t);回響y(t)減去線性回響y2(t)得到的非線性回響y1(t);非線性回響與兩個白噪聲輸入之間的互相關函式h2(τ1,τ2),即二階核。在τ1、τ2平面上的核狀封閉曲線是h2(τ1,τ2)的等值線。
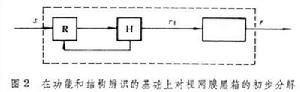
圖1是典型的一、二階核計算方法。圖中是在白噪聲刺激(輸入)下系統的回響曲線y(t);回響曲線的零階核h0(常數),即y(t)的期望值;y(t)減去期望值得到的零均值回響y0;y0與白噪聲的互相關函式h1(τ),即一階核;白噪聲的刺激下一階核的線性回響y2(t);回響y(t)減去線性回響y2(t)得到的非線性回響y1(t);非線性回響與兩個白噪聲輸入之間的互相關函式h2(τ1,τ2),即二階核。在τ1、τ2平面上的核狀封閉曲線是h2(τ1,τ2)的等值線。 白噪聲估計方法的重要性在於:兩個系統一致(即有完全相同的輸入輸出關係)的充分必要條件是它們對正態白噪聲輸入有相同的回響。因此用正態白噪聲估計出來的維納核只要精度足夠高,就可以作為系統的描述,並可用以預測對任何輸入的回響。這種方法著眼於研究缺乏先驗知識、機理不清的非線性系統,適用於研究黑箱。這種方法在生理系統的分析中得到成功的套用。例如在研究脊椎動物視網膜的過程中把刺激-回響試驗(即功能辨識)和解剖學知識 (即結構辨識的先驗知識)結合起來完成視網膜的建模和辨識。先辨識對視網膜的光刺激s和送入大腦的信號r之間的功能關係,這是完全的黑箱方法(圖2虛線部分)。再利用解剖學知識,知道水平細胞H處於從光到神經中樞信息處理的通路中間,然後測量H的回響r1,原系統就分解成兩個子系統。再將電流通入H並記錄視網膜光感受器R 的回響就可證實從H到 R存在反饋。這樣就把視網膜分解成三個子系統並能測出各自的特性。繼續這種分解,逐步打開黑箱便得到完整的視網膜模型(圖3)。圖3中,r3為對雙極細胞B的檢測,r4為對無長突細胞A的檢測。圖4是用所測數據求得的視網膜模型一階核和二階核。
 維納核估計
維納核估計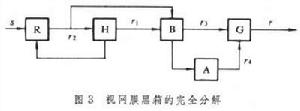 維納核估計
維納核估計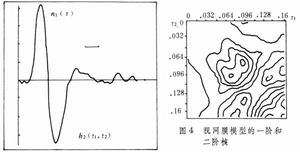 維納核估計
維納核估計