互相關函式
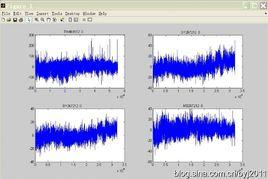
 chen’s系統x序列的自/互相關函式
chen’s系統x序列的自/互相關函式對於連續信號公式表示為 R(τ)=(1/T)∫[f(t)g(t+τ)]dt,積分限為 0至T。
對於離散信號公式表示為 R(n)=(1/N)∑[x(m)y(m+n)]其中 m從 0到N-1變化。
特殊地,若離散信號為二進制信號,互相關函式應表示為 R(n)=(A-D)/(A+D)其中 A、D分別為x序列與循環移 n位後的 y序列之間相同的碼元數和不同的碼元數。
確定信號
定義
令f1(t), f2(t) 為能量信號,一般情況可以是時間的複函數,稱:
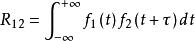 互相關函式
互相關函式為f1(t)和f2(t) 的互相關函式。
套用
互相關函式的上述性質在工程中具有重要的套用價值。
(1) 在混有周期成分的信號中提取特定的頻率成分。
(2) 線性定位和相關測速。
(3) 在圖像配準中的套用(原理介紹):
 互相關函式
互相關函式根據傅立葉變換定理
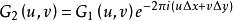 互相關函式
互相關函式根據互相關函式的定義
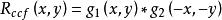 互相關函式
互相關函式有卷積定理可知
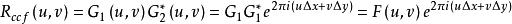 互相關函式
互相關函式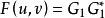 互相關函式
互相關函式其中 ,反傅立葉變換可得
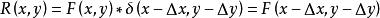 互相關函式
互相關函式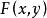 互相關函式
互相關函式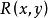 互相關函式
互相關函式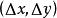 互相關函式
互相關函式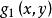 互相關函式
互相關函式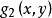 互相關函式
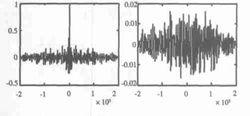
互相關函式由自相關的性質可知,函式的峰值在原點處,因此的峰值出現在點處,也就是函式和的偏移量。
互相關函式的性質
1.R12(t)=R21(-t)
2.對於1、2同周期的函式,相關函式具有相同的周期特性
自相關函式
1. 首先說說自相關和互相關的概念。
這個是信號分析里的概念,他們分別表示的是兩個時間序列之間和同一個時間序列在任意兩個不同時刻的取值之間的相關程度。自相關函式是描述隨機信號X(t)在任意兩個不同時刻t1,t2的取值之間的相關程度;互相關函式給出了在頻域內兩個信號是否相關的一個判斷指標,把兩測點之間信號的互譜與各自的自譜聯繫了起來。它能用來確定輸出信號有多大程度來自輸入信號,對修正測量中接入噪聲源而產生的誤差非常有效。
事實上,在圖象處理中,自相關和互相關函式的定義如下:設原函式是f(t),則自相關函式定義為R(u)=f(t)*f(-t),其中*表示卷積;設兩個函式分別是f(t)和g(t),則互相關函式定義為R(u)=f(t)*g(-t),它反映的是兩個函式在不同的相對位置上互相匹配的程度。
那么,如何在matlab中實現這兩個相關並用圖像顯示出來呢?
dt=.1;
t=[0:dt:100];
x=cos(t);
[a,b]=xcorr(x,'unbiased');
plot(b*dt,a)
上面代碼是求自相關函式並作圖,對於互相關函式,稍微修改一下就可以了,即把[a,b]=xcorr(x,'unbiased');改為[a,b]=xcorr(x,y,'unbiased');便可。
2. 實現過程:
在Matalb中,求解xcorr的過程事實上是利用Fourier變換中的卷積定理進行的,即R(u)=ifft(fft(f)×fft(g)),其中×表示乘法(註:此公式僅表示形式計算,並非實際計算所用的公式)。當然也可以直接採用卷積進行計算,但是結果會與xcorr的不同。事實上,兩者既然有定理保證,那么結果一定是相同的,只是沒有用對公式而已。下面是檢驗兩者結果相同的代碼:
dt=.1;
t=[0:dt:100];
x=3*sin(t);
y=cos(3*t);
subplot(3,1,1);
plot(t,x);
subplot(3,1,2);
plot(t,y);
[a,b]=xcorr(x,y);
subplot(3,1,3);
plot(b*dt,a);
yy=cos(3*fliplr(t)); % or use: yy=fliplr(y);
z=conv(x,yy);
pause;
subplot(3,1,3);
plot(b*dt,z,'r');
即在xcorr中不使用scaling。