簡介
維格納分布(又名 韋格納分布，英文: Wigner Distribution Function,縮寫為 WDF) 是由1963年的諾貝爾物理學獎得主尤金·維格納，於1932年首次引用的一個新的方程式。 眾所皆知，傅立葉變換對於研究穩態(時間獨立)的訊號(波形)是一項非常有用的工具，然而，訊號(波形)一般來說在時間上並非是獨立的，這樣的訊號或是波形傅立葉變換並無法有效地完全分析其特性，因此對於一個非穩態的訊號完全分析需要測量出時間以及頻率上的表現。本頁面介紹的數學函式是時頻分析中的基礎方法，在1980年，Claasen，Mecklenbrauker對WDF做了更進一步的研究。除此之外，線性時頻分析中，STFT、Gabor transform和WDF扮演了相當重要的角色，其中WDF對於分析很多非穩態的隨機訊號都有很好的表現，例如：量子力學、光學、聲學、通訊、生物工程、訊號處理和影像處理。有時也被用在分析地震的資料，以及處理聲音的相位失真。
定義
定義一
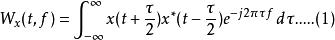維格納分布定義二
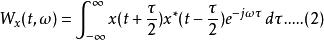維格納分布
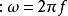維格納分布定義二與定義一之間的關係
其他定義
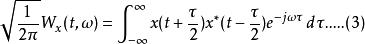維格納分布在聲納和雷達系統中，傳送出去的聲波的反射波可以用來偵測目標物的位置跟速度，在很多情形下，收到的訊號因為都普勒位移，所以跟原本的訊號並不一樣。Woodward(1953) 改寫了原本的公式
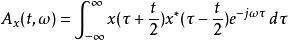維格納分布這個公式被稱為Woodward ambiguity function，這個式子在雷達系統的訊號處理和設計上扮演重要的角色。
WDF和STFT的比較
WDF、STFT和Gabor transform 都占了時頻分析中非常重要的地位，在這邊比較一下它們之間的差別。
| WDF | STFT | |
| 清晰度 | 較好 | 較差 |
| 相交項的問題 | 嚴重 | 無 |
| 複雜度 | 高 | 低 |
相交項其實就是處理的過程中產生的額外訊號，是不想要的，WDF的清晰度和複雜度是彼此做取捨的，可以依不同的情況或是不同的方法來決定是否要使用WDF或是另外兩種。
