貝葉斯定理
貝葉斯定理是關於隨機事件A和B的條件機率和邊緣機率的一則定理。
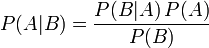
在貝葉斯定理中,每個名詞都有約定俗成的名稱:
P(A)是A的先驗機率或邊緣機率。之所以稱為"先驗"是因為它不考慮任何B方面的因素。
P(A|B)是已知B發生後A的條件機率,也由於得自B的取值而被稱作A的後驗機率。
P(B|A)是已知A發生後B的條件機率,也由於得自A的取值而被稱作B的後驗機率。
P(B)是B的先驗機率或邊緣機率,也作標準化常量(normalized constant).
按這些術語,Bayes定理可表述為:
後驗機率 = (相似度*先驗機率)/標準化常量
也就是說,後驗機率與先驗機率和相似度的乘積成正比。
另外,比例P(B|A)/P(B)也有時被稱作標準相似度(standardised likelihood),Bayes定理可表述為:
後驗機率 = 標準相似度*先驗機率
貝葉斯方法
貝葉斯方法是貝葉斯定理的一種統計解釋,利用它,甚至在先驗 分布(a Priorj distribution)未知時,也可對不能觀察的 參數作出推斷
設(Y,X)為一隨機向量.對隨機參數X 的任何給定值X=x,Y的條件分布密度p伽}x)己知,若 在某一試驗中僅能觀察到Y取的值,而X的相應取值 未知,而需要估計未觀察到的X的一個函式傘伏)
按此方法,條件數學期望E伸(x)}月=功(均應取 為中(x)之近似值,依Bayes公式(B ayes formula),這 期望由公式 、Y)一坦絲半黔竺哩(;) q(Y) 在),而只能得出此函式上下限的估計,它們是通過解出 下述線性規劃問題而求得的:以沙,(Y)和盛(均分別 記(1)式分子中的線性泛函線上性約束P(x))認 知(x)d卜(x)=l和。(Y)二丁p(Ylx)p(x)d拼(x)=今(Y)之下 的最小和最大值(極值是對未知的先驗分布p(x)來取), 其中創Y)是前面提及的q(Y)估計量,由觀察值y、,…, 磯作出.
在這個情況下可證明訪,(Y)/4(Y)蕊價(均續 功2(Y)/場(Y)成立的機率趨於1,如果用於作估計量場(Y) 的隨機變數丫的個數無限增加(據大數律(law of large numbers”.也可能作出經驗Bayes方法的其他修 正—例如,在土述最後一條件仔(Y)二4(Y)之上附加 有限個形如q(y;)二母(只)的條件,其中只是起初給定的 數.若4用q的相應置信限來代替,則條件將有不等式 9.(共)簇q以)落q:以)的形式,等等. 在某些套用上重要的場合,可找到函式價;和價:的 適宜的優控函式,而不必通過費力的線性規劃法(見樣 本法(samPle method)中討論統計控制的例子).
關於將經驗Bayes方法用於涉及隨機參數值的假 設的檢驗,參見判別分析(discriminant analysis). 給出,其中 、妙)=jP妙Ix滬(x)d風x),儀) p(x)是X的無條件(先驗)分布的密度,拜(x)是相應的 叮有限測度,而q砂)是Y的無條件分布的密度. 如果先驗密度未知,則無法計算沙和q之值.但 是,若有為數充分多的,從具密度q印)的分布中抽出的 隨機變數現實藝,…,X為已知,則可以構造出僅依賴於藝, …,長的相合估計4伽).C.H.反卿陰祀湘(【11)提出估計 沙(Y)的方法如下:以4伽)代(2)中的q伽)並求出此積 分方程的解戶(x),然後以戶和4取代(l)式右邊的p 和q.但這種方法很困難,因為求解積分方程(2)是一 在計算數學中難於處理的問題.
在某些特殊情況下,統計的方法不僅可用於估計q, 也可用於估計妙(見〔31).這是可能的,如果包含x和y 的恆等式 毋(x)P妙}x)=又妙)r【:妙)!x](3) 成立.在(3)中,又砂)和:妙)都是僅依賴於y的函式,而 r(z!x)作為z的函式是機率密度(即可視為某隨機變數 Z在給定X=x時的條件密度).若(3)成立,則(l)式的 分子等於又(Y)s[:(y)],其中s(z)=丁r(zlx)p(x)d拼(x) 為Z的無條件分布的密度.這樣,如果有為數充分多的 具密度s(z)的獨立隨機變數現實21,…,虱,則可作出 s(z)的相合估計g(z),從而也可以找到叭Y)的一個相合 估計價(Y): 側泊、“”二雲”=三過且炙以.(4) q(Y) 例如,設需要估計價(X)=X為,其中h為正整數,而 夕(夕Ix)=xye一今夕!伽=0,l,.二,x>0),則職(x)p砂}x)二又伽)· 夕伽+hlx),其中又伽)=(夕+h)!/y!,因為在此有r(z ix)= P公}x),得到s(z)二q(z).相應地有少(Y)=又舊創Y+h)/ 叔Y),即在確定叭Y)時只需有藝,磯,…的值.
另一方 面,如果P伽}x)=b。伽lx)二C二x少(l一x)”一y伽=0,“’,”: 九為正整數:0落x(l,C二=(羅)),則價(x)p。}x)= 又(y)r妙+hlx),其中又(y)二e言/e蓋車交而r(ztx)= 氣+、(z}x)筍P(ylx).由於這個原因,在本例中為作出 叭Y)需要兩個序列試驗值琴和zj· 這個形式的經驗Bayes方法只能用於一個很狹小 的族,其中密度P伽}x)和函式價(x)適合條件(3).但即 使這條件確實滿足,估計量(4)的構造仍取決於隨機變 量zj的可觀察性,而通常zj的密度與藝的密度不同, 藝是直接觀察到的·為了實用的目的,更可取的是在一 種修改過的形式下使用經驗Bayes方法,這時不存在 上述不便之處.
