經驗正交函式

經驗正交函式分析方法(Empirical Orthogonal Function,縮寫為EOF)，也稱特徵向量分析(Eigenvector Analysis)，或者主成分分析(Principal Component Analysis,縮寫PCA)，是一種分析矩陣數據中的結構特徵，提取主要數據特徵量的一種方法。Lorenz在1950年代首次將其引入氣象和氣候研究，現在在地學及水聲學等其他學科中得到了非常廣泛的套用。地學數據分析中通常特徵向量對應的是空間樣本，所以也稱空間特徵向量或者空間模態；主成分對應的是時間變化，也稱時間係數。因此地學中也將EOF分析稱為時空分解。

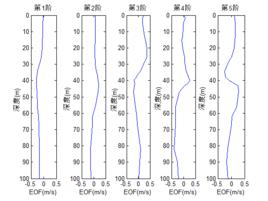
E0F分析方法能夠把隨時間變化的變數場分解為不隨時間變化的空間函式部分以及只依賴時間變化的時間函式部分。空間函式部分概括場的地域分布特點，而時間函式部分則是由場的空間點的變數線性組合所構成，稱為主要分量。這些分量的頭幾個占有原場內空間點所有變數的總方差的很大部分，這就相當於把原來場的主要信息濃縮在幾個主要分量上，因而研究主要分量隨時間變化的規律就可以代替場的時間變化研究，且可以通過這一分析得出的結果來解釋場的物理變化特徵。它的優點在於典型場由變數場序列本身的特徵來確定，而不是事先人為規定，因而能較好地反映出場的基本結構。這種方法展開收斂速度快，很容易將大量資料信息濃縮集中。它能對有限區域內不規則分布的站點進行分解，且分解的空間結構具有明確的物理意義。Lorenz在20世紀50年代首次將其引入氣象和氣候研究，現在該方法已在海洋和其他學科中得到了廣泛的套用。