統一強度理論的力學模型
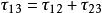 統一強度理論
統一強度理論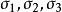 統一強度理論
統一強度理論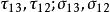 統一強度理論
統一強度理論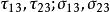 統一強度理論
統一強度理論考慮到 , 即三個主剪應力中只有兩個獨立分量,統一強度理論將一般主應力狀態( )轉換為雙剪應力狀態( )或( ),建立了一種新的正交八面體的雙剪單元體力學模型,即統一強度理論力學模型,如圖1所示。
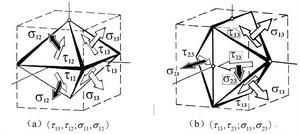 圖1 統一強度理論的力學模型
圖1 統一強度理論的力學模型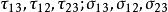 統一強度理論
統一強度理論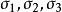 統一強度理論
統一強度理論圖1中的所有應力分量( )和主應力( )之間的關係為
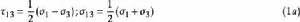 統一強度理論
統一強度理論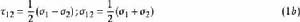 統一強度理論
統一強度理論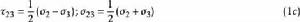 統一強度理論
統一強度理論統一強度理論的數學建模
從雙剪力學模型出發,考慮到雙剪單元體上所有剪應力和正應力分量以及它們對材料破壞的不同貢獻,建立統一強度理論的數學建模方程為:
 統一強度理論
統一強度理論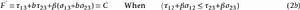 統一強度理論
統一強度理論 統一強度理論
統一強度理論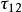 統一強度理論
統一強度理論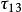 統一強度理論
統一強度理論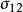 統一強度理論
統一強度理論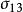 統一強度理論
統一強度理論式(2a)、(2b)中 為反映正應力對材料破壞的影響係數;C為材料的強度參數;b為反映中間主剪應力 或 以及相應的正應力 或 作用的係數,如圖1所示。
統一強度理論數學建模方程中參數的實驗確定
 統一強度理論
統一強度理論統一強度理論數學建模方程(2a)、(2b)中參數 和C可以由材料的拉伸強度和壓縮強度確定。材料的單軸拉伸和單軸壓縮的應力狀態分別為:
 統一強度理論
統一強度理論 統一強度理論
統一強度理論 統一強度理論
統一強度理論將式(1a)、(1b)和(3a)代入(2a)、式(1a)、(1c)和(3b)代入(2b)可得統一強度理論的參數 和C的值為:
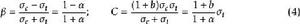 統一強度理論
統一強度理論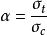 統一強度理論
統一強度理論式(4)中 為材料的拉壓強度比。
統一強度理論的主應力表達式
將材料參數公式(4)和雙剪單元體應力公式(1a)、(1b)代入數學建模方程(2a)、材料參數公式(4)和雙剪單元體應力公式(1a)、(1c)代入數學建模方程(2b),即可得到統一強度理論的主應力表達式為:
 統一強度理論
統一強度理論 統一強度理論
統一強度理論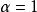 統一強度理論
統一強度理論對於拉壓強度相同的金屬類材料( ),統一強度理論簡化為只有一個參數的統一屈服準則:
 統一強度理論
統一強度理論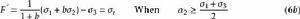 統一強度理論
統一強度理論統一強度的理論的極限面和極限跡線
統一強度理論在主應力空間的極限面由一系列有序變化的極限面所構成,如圖2a所示。當材料拉壓強度比為1時,統一強度理論極限面不等邊多面錐體簡化為無限長的柱體如圖2b所示。統一強度理論的一系列外凸極限面可以十分靈活地適用於各種不同的材料。
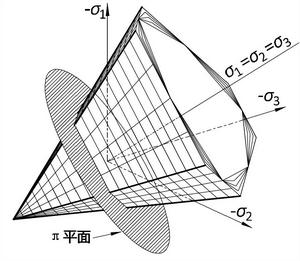 統一強度理論
統一強度理論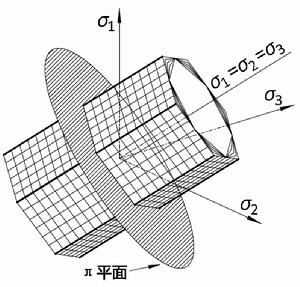 統一強度理論
統一強度理論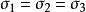 統一強度理論
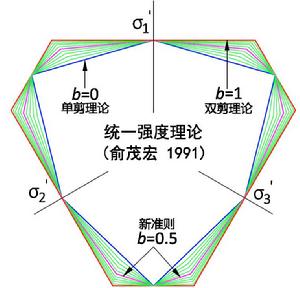
統一強度理論主應力空間中與三個坐標軸傾角相等的軸稱為靜水應力軸(即 軸),與靜水應力軸垂直的面稱為偏平面,空間極限面與偏平面相交的跡線稱為偏平面極限跡線。統一強度理論和統一屈服準則的偏平面極限跡線分別如圖3a和圖3b所示。
 統一強度理論
統一強度理論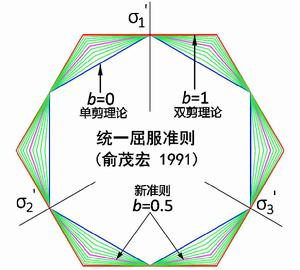 統一強度理論
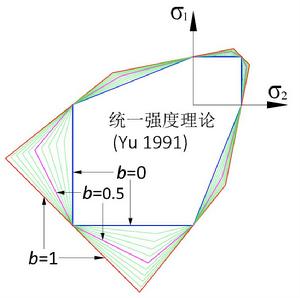
統一強度理論統一強度理論和統一屈服準則在平面應力狀態下的極限跡線分別如圖4a和圖4b所示。
 統一強度理論
統一強度理論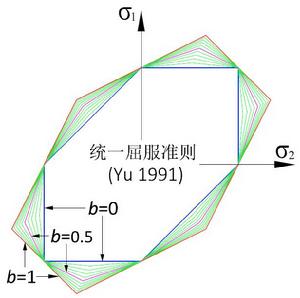 統一強度理論
統一強度理論研究歷史
統一強度理論的研究經歷了漫長的過程。早在1901年,德國哥廷根大學教授沃伊特就認為,對於各種不同材料套用一個強度理論是不可能的。1953年,史丹福大學教授鐵木辛柯在他的材料力學發展史中寫道:“沃伊特進行了大量複雜應力實驗,以校核莫爾的理論,試驗的材料均為脆性材料,所得結果並不與莫爾的理論相符合。沃伊特由此得出結論,認為強度問題是非常複雜的,要想提供一個單獨的理論有效地套用到各種建築材料上是不可能的”。這就是“沃伊特-鐵木辛柯難題” (Voigt-Timoshenko Conundrum)。1985年,中國大百科全書力學篇也認為:“想建立一種統一的、適用於各種工程材料和各種不同的應力狀態的強度理論是不可能的”(第二版已將這段話刪除)。同年俞茂宏在《中國科學》發表的文章中也認為:“似乎還不可能用單一的理論或準則去說明各種不同材料在複雜應力狀態下的破壞和滑移現象”。
同時,前蘇聯科學院院士達維堅科夫和弗里德曼於20世紀40年代提出了一種企圖套用於各種材料的統一強度理論(也可譯為聯合強度理論)。聯合強度理論在東歐和中國有很大推廣。改革開放以後,人們開始一些新的認識。1985年中國大百科全書力學篇指出達維堅科夫和弗里德曼的聯合強度理論只是“有區別地選用已有的最大剪應力理論或最大伸長應變理論,所以它實質上只是提供一個選用現成強度理論的方法”。
沃伊特-鐵木辛柯統一強度理論難題的破解得益於德魯克公設和雙剪理論的思想。1951年德魯克提出一個塑性的基本公設,稱為德魯克公設。由此可以得出強度理論的外凸性。它為強度理論的研究奠定了理論框架。1991年俞茂宏在日本京都召開的第6屆國際材料力學會議上發表了一篇《材料在複雜應力狀態下屈服和破壞的新模型和新理論》,提出了一個新的強度理論公式,就是現在的統一強度理論。
可以用三個不同階段的強度理論來說明統一強度理論的發展過程:
1、 雙剪屈服準則:
適用於拉壓強度相等的材料,由俞茂宏於1961年提出:
 統一強度理論
統一強度理論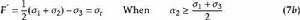 統一強度理論
統一強度理論2、 雙剪強度理論:
適用於壓縮強度大於拉伸強度的材料,由俞茂宏於1985年提出:
 統一強度理論
統一強度理論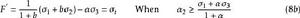 統一強度理論
統一強度理論3、統一強度理論:
可適用於壓縮強度大於拉伸強度的材料,覆蓋了外凸區域從內邊界到外邊界的全部範圍,表達式見(5a)、(5b),由俞茂宏於1991年提出:
可以看出,統一強度理論發展三個階段的表達式非常相近,而他們之間的區別正好反映了統一強度理論的發展歷史。
意義
統一強度理論已經在土木、水利、機械、航空、岩土等工程結構研究中得到較為廣泛的套用。它得到的一系列結果的可以適用於不同的材料和結構。統一強度理論的套用可以充分發揮材料和結構的強度潛力,具有巨大的經濟意義。統一強度理論已經擴展套用到其它領域,如《廣義塑性力學》、《結構塑性力學》和《計算塑性力學》,它的套用可以充分發揮材料和結構的強度潛力,具有巨大的經濟意義。
