基本介紹
終邊相同的角是指頂點為平面直角坐標系中的原點,始邊為X軸的正半軸,具有相同的終邊的角。所有與a角終邊相同的角,連同a角在內(而且只有這樣的角),可以用式子k·360°+a或者2kπ十a,k∈Z來表示。就是說,對於給定的頂點、始邊和終邊,確定了一個由無限個角組成的集合。與a角終邊相同的角的集合可以記作{β|β=k·360°+a,k∈Z}或{β|β=2kπ+a,k∈Z}。終邊在X軸上的角的集合可記作{β|β=k·180°,k∈Z}或者{β|β=kπ,k∈Z}。終邊在Y軸上的角的集合可記作{β|β=k·180°+90°,k∈Z}或者{β|β=kπ+π/2,k∈Z} 。
 終邊相同角
終邊相同角相關分析
 終邊相同角
終邊相同角 終邊相同角
終邊相同角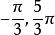 終邊相同角
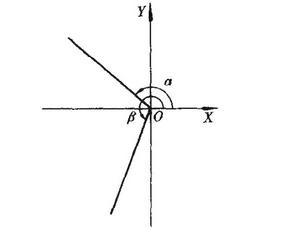
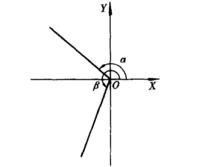
終邊相同角把角放在直角坐標系裡的標準位置,即使角的頂點與坐標原點重合,角的始邊與x軸的正半軸重合,角的終邊在第幾象限,就把這個角叫作第幾象限角(或說這個角在第幾象限)。如圖1中,和都是第一象限的角,在圖2中是第四象限的角 。
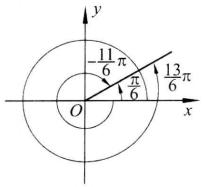 圖1
圖1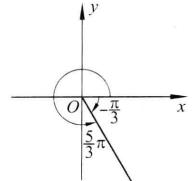 圖2
圖2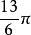 終邊相同角
終邊相同角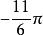 終邊相同角
終邊相同角 終邊相同角
終邊相同角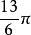 終邊相同角
終邊相同角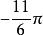 終邊相同角
終邊相同角在圖1中,可以看出與都和的終邊相同。和可以寫成下列形式:
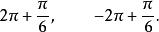 終邊相同角
終邊相同角 終邊相同角
終邊相同角顯然,除了這兩個角以外,與的角終邊相同的角還有:
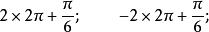 終邊相同角
終邊相同角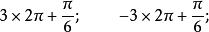 終邊相同角
終邊相同角 終邊相同角
終邊相同角 終邊相同角
終邊相同角 終邊相同角
終邊相同角所有和的角終邊相同的角,連同在內,可以用下式表示:
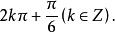 終邊相同角
終邊相同角 終邊相同角
終邊相同角 終邊相同角
終邊相同角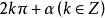 終邊相同角
終邊相同角一般地,所有和角 終邊相同的角,連同在內,可以用式子來表示。
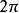 終邊相同角
終邊相同角 終邊相同角
終邊相同角 終邊相同角
終邊相同角由此可見,具有相同終邊的角有無限多個,它們彼此之間相差整數個周角,即的整數倍,與角終邊相同的角(角處在標準位置)的集合可記作
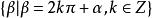 終邊相同角
終邊相同角 終邊相同角
終邊相同角(以弧度制給出)
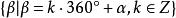 終邊相同角
終邊相同角或(a以角度制給出) 。
例題解析
【例1】在0°到360°的範圍內,找出與下列各角終邊相同的角,並判定下列各角是哪個象限的角 。
(1)﹣120°; (2)640°; (3)﹣950°12'.
解 (1)因為﹣120°=-360°+240°,所以-120°的角與240°的角的終邊相同,它是第三象限的角;
(2)因為640°=360°+280°,所以640°的角與280°的角的終邊相同,它是第四象限的角;
(3)因為-950°12'=-3×360°+129°48',所以-950°12'的角與129°48'的角的終邊相同,它是第二象限的角。