納維－斯托克斯方程

納維－斯托克斯方程是牛頓第二定律在不可壓縮粘性流動中的表達式。簡稱N-S方程。

納維－斯托克斯方程

正文

牛頓第二定律在不可壓縮粘性流動中的表達式。簡稱N-S方程。此方程是法國力學家、工程師C.-L.-M.-H.納維於1821年創立，經英國物理學家G.G.斯托克斯於1845年改進而確定的。它的矢量形式為：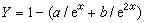

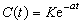
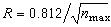
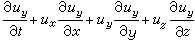
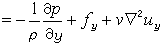
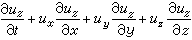
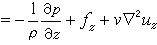
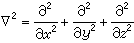在直角坐標中的分量形式為：

式中ρ、ν、p、u、f分別為液體密度、運動粘性係數、動水壓強、流速矢量、單位質量的質量力;墷為矢量微分算符；為拉普拉斯算符。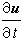為指定點處由於時間改變而引起的速度變化率，稱為當地加速度；(u·墷)u 為指定瞬時由於空間位置改變而引起的速度變化率,稱為遷移加速度;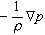與ν墷2u分別為作用於單位質量液體表面的合壓力與合粘性力；(ux,uy,uz)及(fx,fy,fz)為u及f在直角坐標中的投影。
在某些情況下，合粘性力很小，可忽略不計，於是N-S方程簡化為理想液體的歐拉方程。即：

對於需作流場分析的水力學問題,N-S方程有特別重要的意義。它和三維連續性方程一道組成不可壓縮粘性流動完整方程組，附加一定的初始條件和邊界條件，從理論上講,就可以解出流速分布和壓強分布。但N-S方程是非線性的二階偏微分方程，僅在一些特定條件下，才能求出解析解。對於低雷諾數流動，可全部地或部分地略去慣性項，求得蠕動流近似解。對高雷諾數流動，在物體表面附近的邊界層內，必須考慮粘性影響，按邊界層方程求解；邊界層外，粘性效應可以忽略，用歐拉方程近似求解。在很多情況下，特別是中等雷諾數的流動，可求出N-S方程的數值解。大型電子計算機的套用,為N-S方程的數值解開闢了廣闊的前景。

配圖

相關連線