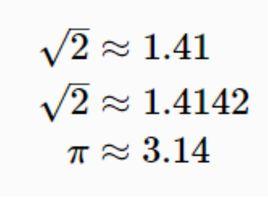基本介紹
用來表示量的準確值的數叫做準確數。
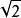 精確數
精確數 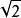 精確數
精確數 在計算中,我們遇到的數值通常有兩種:一種是完全精確的數(真值),稱為精確數或準確數;一種是近似數(近似值),,它是與精確數非常接近、相差很小的數。如用1.41、1.4142代替無理數,這裡是精確數(真值),而1.41、1.4142都是近似值。
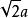 精確數
精確數 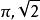 精確數
精確數 精確數是指沒有誤差的數。如某正方形的邊長為a,則其周長為4a。其中的4即是精確數,它沒有誤差。常用整數或分數表示精確數,但精確數也可使用小數或無理數表示。如1mm=0.001m,此處的0.001即是精確數。直徑為D的圓的周長為πD,邊長為a的正方形的對角線長度為。此處,也是精確數。但在計算中,無理數常使用有限精度的小數參與運算,這時,參與運算的無理數就成了近似數。含有誤差的數值,統稱為近似數。近似數的精度,使用有效數字描述 。
相關概念
近似值:近似於準確值的值稱為近似值。較準確值小的近似值稱為不足近似值,較準確值大的近似值稱為過剩近似值 。
近似數:用來表示量的近似值的數叫做近似數。
誤差:近似數與它的準確數之差稱為誤差。誤差按其來源可分為測量誤差、截斷誤差和舍人誤差。
絕對誤差:一個近似數與它的準確數的差的絕對值叫做這個近似數的絕對誤差。用a表示近似數,A表示它的精確數,那么近似數a的絕對誤差就是|a-A|。
相對誤差:一個近似數的絕對誤差對於它的準確數所占的百分數,叫做這個近似數的相對誤差。用a表示近似數,A表示它的精確數,那么近似數a的相對誤差就是
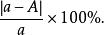 精確數
精確數 相對誤差能確切地表示近似值的近似程度。在不知道準確數的情況下,我們就用絕對誤差對近似數所占的百分數作為這個近似數a的相對誤差。
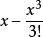 精確數
精確數 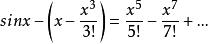 精確數
精確數 截斷誤差:在一般計算問題中,為了便於計算,將複雜的表達式用一近似表達式來代替,而稱正確表達式與近似表達式之差為截斷誤差。例如,用代替sinx時,截斷誤差為
捨入誤差:在計算過程中出現的位數較多的數,往往為了計算方便或是受到計算工具的限制,要用位數較少的數來代替。代替的方式通常採用四捨五入、只舍不人等規則。由此產生的誤差稱為捨入誤差。
例如,用3.14代替3.14159265 ...時,舍人誤差為0.00159265...。
四舍五人法:一種近似數的截取法。其方法是把要處理的數保留到某一指定的數位為止,後面的數字全部捨去, 如果捨去的第一位數字是5或者大於5,在保留的最後一位數字上加1;如果捨去的第一位數字小於5,保留的數就不變。
去尾法:一種近似數的截取法。其方法是,把要處理的數保留到某一指定的數位為止,後面的數字全部捨去。
例如,3. 14159...用去尾法截取到千分位(即精確到0.001 )就得近似數3.141。
進一法:一種近似數的截取法。其方法是,把要處理的數保留到某一指定的數位為止,後面的數字全部捨去,但是如果捨去的數字不都是零,那么保留的最後一位數字上加1。
例如,5. 43106用進一法截取到千分位,就得近似數5.432
抹尾湊整法:一種近似數的截取法。抹尾湊整規則是:要把一個數抹尾湊整到n位有效數字,就須先把這個數的第n位右邊的全部數字都抹去,(1)如果被抹去的部分大於第n位數字的半個單位,則在第n位數字上加1; (2)如果小於第n位數字的半個單位,則保持第n位數字不變;(3)如果恰好是第n位數字的半個單位,則當第n位數字為奇數時就加1;為偶數時就不變。當某一個數按此規則抹尾湊整時,我們就說它精確到n位有效數字。
例如,將1.34996抹尾湊整到5位有效數字為1.3500;4位有效數字為1.350;3位有效數字為1.35;2位有效數字為1.3(1.34996中4996小於1/10位的半個單位)。
上述抹尾湊整的方法可歸結為“四捨六入,五湊偶”,這種規則比舊的四舍五人規則誤差小。
有效數字:一個近似數的絕對誤差,如果不大於它最末一位的半個單位,那么這個近似數從左邊第一個不是0的數字起,到末位數字為止,所有的數字都叫做這個近似數的有效數字。
例如,0.009995的近似值0.01000有四個有效數字1、0、0、0。
用四舍五人法截取得到的近似數,從第一個不是0的數字起到保留的數位為止,所有的數字都是有效數字。
例如,0.0016有兩個有效數字1,6;1.60有三個有效數字1,6,0;1.6有兩個有效數字1,6。這裡1.60比1.6的精確度高。
如果一個近似數是整數,而且末尾帶有幾個0,則必須指明這個近似數精確到哪一位,才能確定它有幾個有效數字。
例如,15000精確到百位,它有3個有效數字1,5,0;一般地用15000 (±50)或者1.50x10 來表示。
準確度和精確度:準確度一由有效數字的個數來確定;精確度——由末一位有效數字的單位來確定。如101.7就說它準確到四位有效數字;它的末一位有效數字是小數點後1位,就說它精確到小數後1位。又如,1.234,12. 34,123.4三個數都準確到四位有效數字,但它們的精確度不同,第1個數最精確; 而三個數1.234,0.234,0.034的精確度雖然相同,都精確到小數點後第3位,但準確度不同,第1個數最準確。
在進行近似數的加減時,我們應考慮精確度;在進行近似數的乘除運算時,決定結果的可靠程度是準確度(有效數字)。所以二者在近似計算中要結合起來運用。
科學計數法:是一種科學技術上常用的記數法。它是把一個正數記成ax10 的形式,其中1≤a