精確對角化法背景
在量子力學中的一個量子系統,物理學家最有興趣的是找出這個量子系統的基態,也就是能量本徵值最小的態,例如:兩個自旋1/2的粒子所形成的量子系統中,若粒子之間的互動作用可寫成
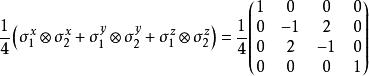 精確對角化法
精確對角化法 精確對角化法
精確對角化法 精確對角化法
精確對角化法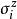 精確對角化法
精確對角化法 精確對角化法
精確對角化法其中 、 、 表示第 個自旋的包立矩陣。將上面4×4的矩陣對角化後可得本徵值:
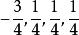 精確對角化法
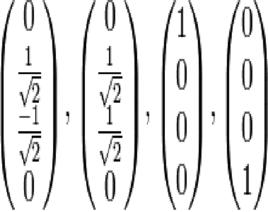
精確對角化法對應的本徵向量為
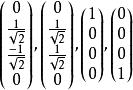 精確對角化法
精確對角化法而
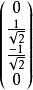 精確對角化法
精確對角化法即為這個系統中的基態。
可想而知,隨著量子系統的粒子數變多,且互動作用愈來愈複雜時,量子系統的基態很難用解析的方法計算出來,因此許多物理學家轉向利用數值方法來求得基態。
精確對角化法難點
精確對角化法(exact diagonaliation)是一個最直接求得基態的數值方法,但由於將哈密頓算符完整對角化非常花費時間與電腦記憶體,所以當需要的只是基態和少數激發態,通常利用Lanczos算法和Davidson算法。 精確對角化法本身的物理概念極為簡單,若是只需要得到極小尺寸的結果,在程式撰寫方面也很容易,然而增加系統尺寸時,隨著所需的記憶體暴增,程式設計變得非常困難。主要困難之處在於如何有效運用有限的記憶體,以及提升程式運作的效率。目前電腦的條件下,精確對角化法的尺寸極限如下:
一維自旋-1/2的環:36個格點。
二維自旋-1/2的平方晶格:40個格點。
二維t-J模型的平方晶格:32個格點,4個電洞。
二維Hubbard模型的平方晶格:32個格點。
一維Holstein 鏈:14個格點。
1.一維自旋-1/2的環:36個格點。
2.二維自旋-1/2的平方晶格:40個格點。
3.二維t-J模型的平方晶格:32個格點,4個電洞。
4.二維Hubbard模型的平方晶格:32個格點。
5.一維Holstein 鏈:14個格點。