玻色子
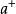 粒子數表象
粒子數表象 粒子數表象
粒子數表象通過定義玻色子升算符 ,降算符 ,以及有n個粒子的態矢量|n>。
由玻色統計中對易關係知:
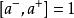 粒子數表象
粒子數表象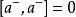 粒子數表象
粒子數表象 粒子數表象
粒子數表象我們可以有以下關係:
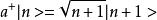 粒子數表象
粒子數表象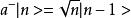 粒子數表象
粒子數表象最終我們可以得到歸一化的玻色子粒子數完備正交矢{|n>}:
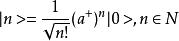 粒子數表象
粒子數表象粒子數算符可以表達為:
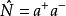 粒子數表象
粒子數表象費米子
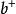 粒子數表象
粒子數表象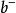 粒子數表象
粒子數表象通過定義費米子升算符 ,降算符 ,以及有n個粒子的態矢量|n>。
由費米統計中反對易關係知:
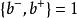 粒子數表象
粒子數表象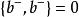 粒子數表象
粒子數表象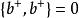 粒子數表象
粒子數表象我們可以有以下關係:
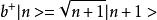 粒子數表象
粒子數表象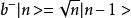 粒子數表象
粒子數表象最終我們可以得到歸一化的費米子粒子數完備正交矢{|n>}:
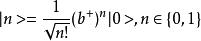 粒子數表象
粒子數表象注意對於費米子而言,由於泡利不相容原理,n只能取0或1,且:
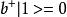 粒子數表象
粒子數表象粒子數算符可以表達為:
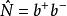 粒子數表象
粒子數表象套用
相對於波函式的表達方式,粒子數表象極大地簡化了書寫,而且在這一表象下,自然而然可以引出二次量子化。
粒子數表象在有關統計學的問題中被廣泛套用。比如光學、凝聚態等領域都會經常使用這一表象來表述問題。
